Network Tied Arch Bridges

Network Tied Arch Bridges

Table of Contents

1. Introduction

2. Efficiency of Network Arches

3. Case Study: Comparison of Network Tied Arch Bridge with Conventional Tied Arch Bridge

4. Conclusion

1. Introduction

Network tied arches are tied arch bridges with inclined hangers where hangers intersect other hangers at least twice. Network tied arch as a concept was developed by Dr. Per Tveit. The world’s most slender arch bridge, The Brandanger Bridge, situated in the western part of Norway, was designed by Dr. Per Tveit and was opened in 2010 (Fig 1). Before this, bridges with inclined hangers were made popular by Nielsen – Lohse (Fig 2). However, these bridges had a drawback in the case of dynamic loads. Under dynamic load, the tension in inclined hangers is reduced, leading to compression in some hangers. The network tied arch developed by Dr. Tveit with multiple crossing of hangers avoided this issue.

Figure 1. The Brandanger network arch bridge (span 220m) in western Norway.

Figure 2. Arch bridge with inclined hangers. One-sided load makes the dotted hangers relaxed.

The compression in the hangers can be avoided by increasing the distance between the nodal points. However, increasing the distance will increase the bending moment in the chords, thus reducing the buckling capacity of the arch. Between the hangers, the arch tends to move up, and the tie tends to move down. An extra set of hangers will reduce the buckling length in the arch and tie, resulting in less bending in the arch. This effect is even more significant if we put three sets of hangers (Fig 3). We arrive at network tied arch geometry with some of the hangers intersecting at least two other hangers with this arrangement.

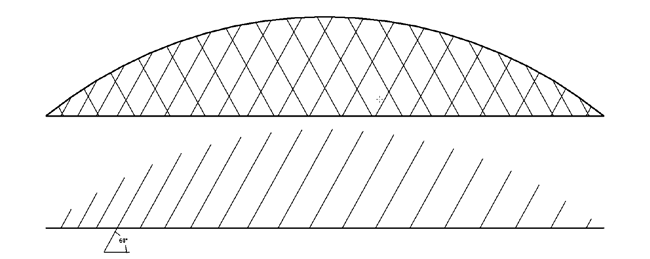Figure 4. Constant slope of hangers

Variable Slope Configuration: In this case, the slope of the hanger varies following a function. A general case is illustrated below.

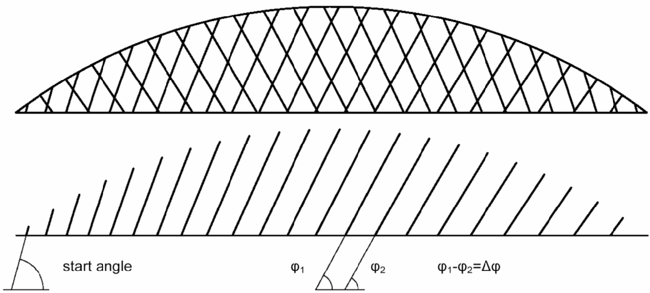Figure 5. Variable slope configuration

Advanced Hanger Configuration: When subjected to UDL, the forces in the hanger are minimized when they are in a radial direction like in a ‘spoked wheel.’ Below shown (Fig 6) is a modified version of the ‘spoked wheel’ model. For such arrangements, if forces in each hanger are approximately equal, the resulting forces will lie on the radii of the arch circle.

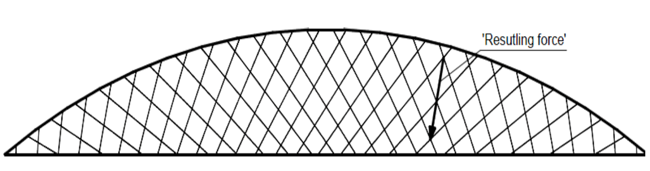Figure 6. Advanced hanger configuration

3. Case Study:

Comparison of Network Tied Arch Bridge with Conventional Tied Arch Bridge

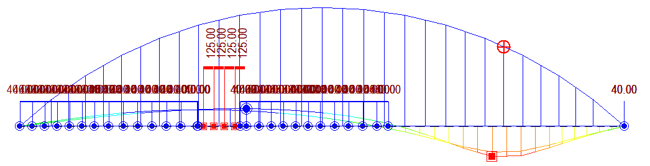
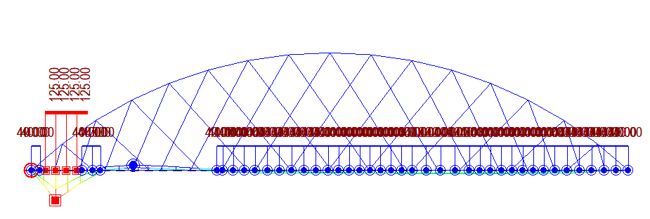
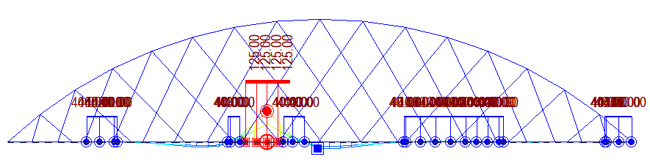
This case study will look at the forces, moments, and deformation in arch and tie beams of network and conventional arch bridges under static and live load. The bridge configuration considered for the case study is shown in fig 7. A similar configuration of the bridge is considered for both cases. Span considered is 91.44 m (300 ft), and the arch rise considered is 18m. All the arch, tie, crossbeams, and cables sections are kept the same for both cases.

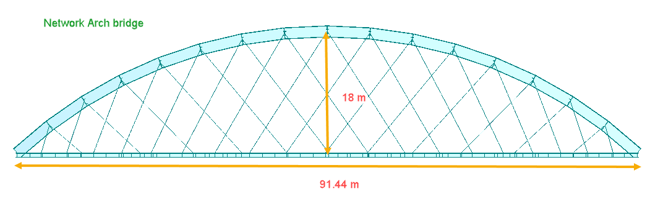
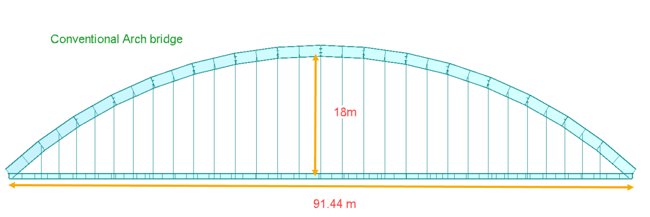
For live loads, a single lane of LM 71, rail traffic load as per Eurocode is considered on the bridge.

In conventional arch bridges, all the hangers are vertical, and they are less in number than the network arch bridge. But for the sake of comparison, we will consider the same number of hangers for both configurations. The results of the following two cases will be checked:

• LC 1: Self-weight and SIDL
• LC 2: Self-weight, SIDL, and Live Loads
  

The decisive force for an arch bridge is axial load and bending moment (in arch and tie). Axial load is the function of the span of the bridge and arch rise. As they are the same for both the bridges, axial loads are also similar. However, the longitudinal moment shows the critical difference in the load-carrying pattern of both the bridges.

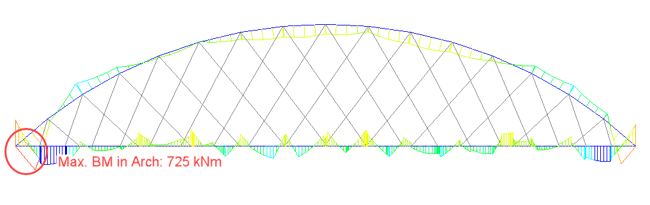
Fig 8 compares the bending moment in the arch and tie due to the LC1 (self-weight and SIDL). A uniform loading is considered throughout the span. The load is predominantly transferred to the arches through the hangers for conventional arch bridges, causing bending moments in the arches. On the other hand, there is no significant bending moment in arches and ties in the case of network arch bridges. For LC 1, the bending moment ratio between the network arch and the conventional arch is 1:6 for arch and 1:3 for tie beams.

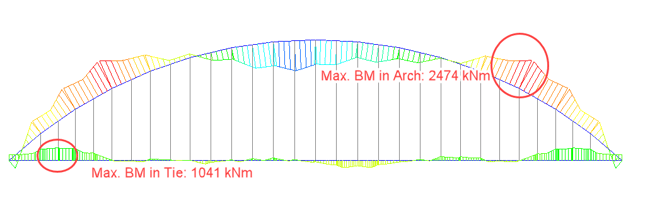
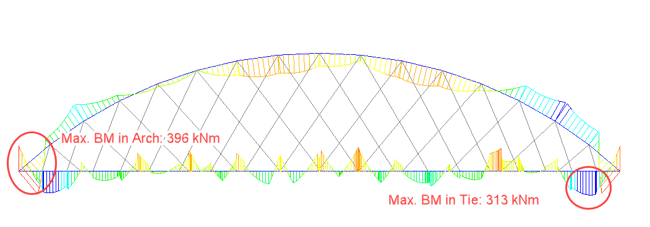
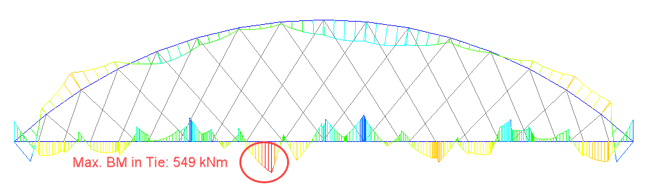
For LC 2, LM 71 live load vehicle on a single track is considered. Fig. 9 and 10 show the maximum bending moment in tie and arch due to LC 2 and the critical position of the vehicle causing this bending moment for both types of arch bridges. Like LC 1 case, the load is predominantly carried by arches and tie beams for conventional arch bridges. However, in the case of network arch bridges, the load sharing is even, and the cross girders connecting the tie beams carry a significant amount of load. Therefore, network arch bridge decks are designed for transverse bending rather than longitudinal bending. For LC 2, the bending moment ratio between the network arch and the conventional arch is 1:7.5 for arch and 1:4 for tie beams.

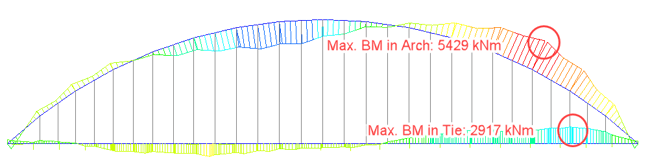
4. Conclusion

Clearly, the above comparison shows that network arch bridges are more efficient than conventional arch bridges. Network arches are stiffer structures due to higher redundancy, and inclined hangers result in better moment and shear distribution in the structure. This can lead to slender arch sections and slimmer tie beams, leading to up to 45% savings in material cost compared to conventional bridges. Network arches are not sensitive to uneven settlements as well. High strength and low weight make network arch bridges dynamically robust structures. Hence network tied arch bridges are clearly a better choice as compared to conventional arch bridges.