Analysis of Reinforced Concrete Solid Slab Bridge

Please fill out the Download Section (Click here) below the Comment Section to download the Full Webinar Presentation File 

This case study covers the following aspects:

1. Introduction to Reinforced Concrete Solid Slab Bridge

2. Bridge Type

3. Computer Modeling Concepts

4. Analysis & Results using MIDAS.

5. Design & Optimization

1. Introduction to RC Solid Slab Bridge

Concrete raw materials, consisting of water, fine aggregate, coarse aggregate, and cement are found in most parts of the world and can be mixed to form a variety of structural shapes. The high availability and flexibility of concrete material and rebar have made the reinforced concrete bridge a very competitive alternative. Reinforced concrete bridges can be made of precast concrete elements, which are fabricated in a production plant and then transported for erection on the job site, or cast-in-place concrete, which is formed and cast directly at its setting location. Cast-in-place concrete structures are often built monolithically and continuously.

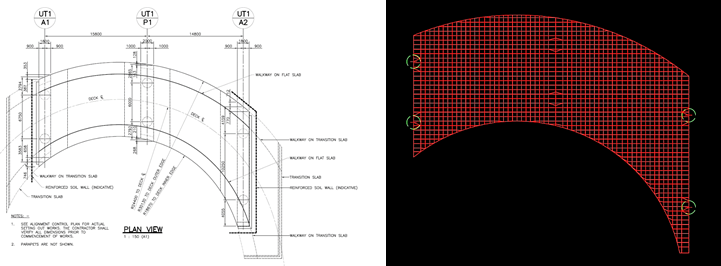
Solid slab bridges are essentially concrete into which internal stresses of the appropriate magnitude and distribution are introduced so that stresses resulting from external loads are counterbalanced to the desired degree. Longitudinally reinforced slab bridges have the simplest superstructure configuration and the polished appearance. This type of solid slab is generally suitable for bridges with a span of up to 15 m.

The behavior of the solid slab is to distribute the applied loads in all directions. The solid slab is isotropic that means it is continuous and uniform in mechanical properties in all directions. Slab bridges could be “anisotropic” also such as “orthotropic” slabs. Some of the examples for this type of slab are shown below.

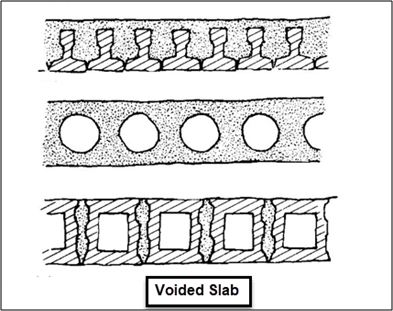
2. Bridge Type 

A. Superstructure Configuration

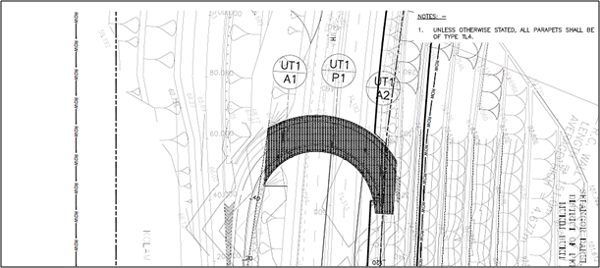
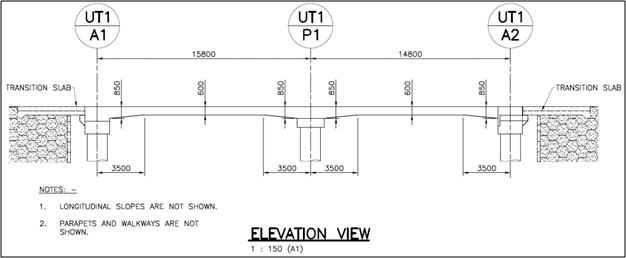
Both the spans have different lengths.

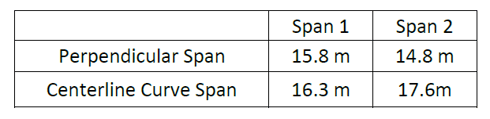
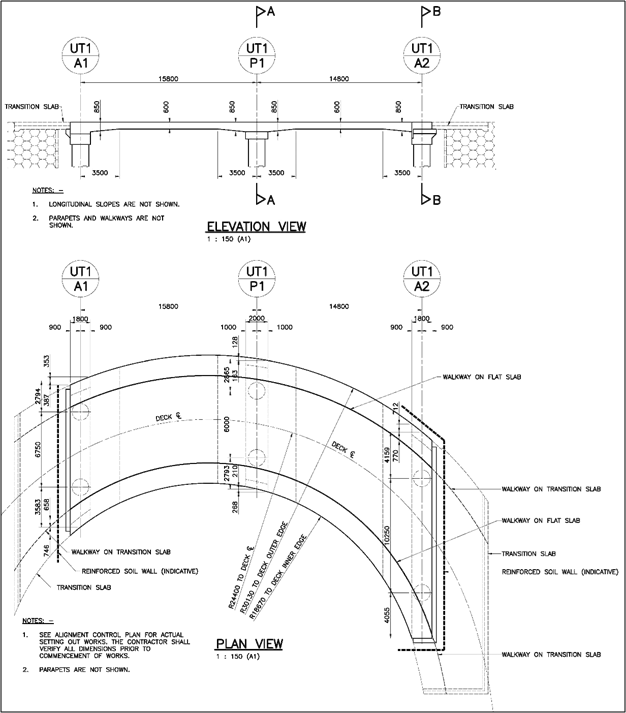
B. Substructure Configuration

All 3 piers are different.

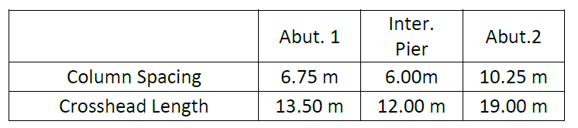
C. Reason for selecting solid slab type

• Short span length (around 15 m)

• Tight radius as straight beams would give too long cantilever slabs at curved edges. Precast curve beams are not practically available and In situ curve beams more difficult to construct.

• Great ability to be built to suit irregular shapes

• Less expensive than more complex types of superstructure.

• Generally, a solid slab deck is more “constructable”.

• Solid slab deck is much heavier in self-weight than other more complex types of deck. When the spans are short (± 15 m), the savings in cost, time, construction simplicity, etc. can more than compensate for the heavier material costs.

3. Computer Modeling Concepts

To model this structure in any structural analysis software, first, we need to decide the modeling methodology. In general, engineers follow two types of methodologies for the solid slab bridge: The grillage model & the plate model.

In the grillage model, 1D beam elements could be used to define the beams in two directions to simulate the longitudinal as well as the transverse stiffness of the bridge. This method provides ease in terms of modeling & result extraction but parallelly, good engineering understanding is required to simulate the solid slab behavior through the beam elements only.

In the plate model, 2D plate elements would be used to simulate the slab that actually represents more realistic slab behavior and give more reliable results. The complexity level of modeling & result extraction is a little bit more as compared to the grillage model. With the help of FEA-based software programs like midas Civil, plate modeling becomes quite easy. For this bridge, plate modeling has been considered and midas Civil has been used for further process.

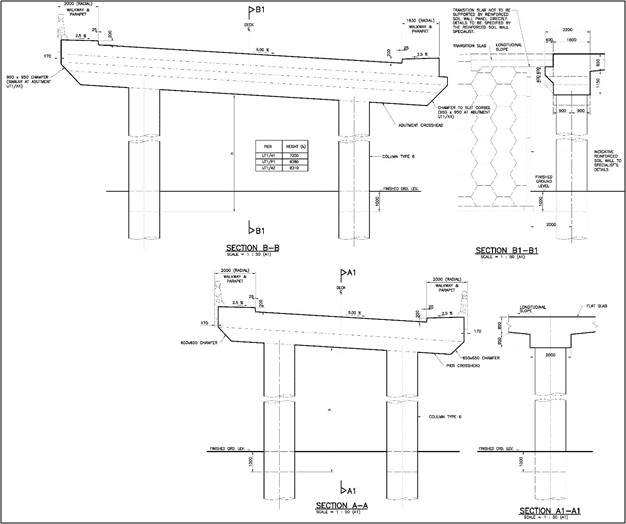
A. Model Geometry :

The model can be generated by using self-built-in tools of the software or if the software has a CAD interface then import the CAD file. As Midas Civil is compatible with the CAD programs, therefore for the modeling, the Bridge deck and crossheads are imported from .dxf; bridge columns and piles are conveniently created by using Midas Civil tools. The shape of elements is basically square quadrilateral elements which are orthogonally matching the intended reinforcement directions. Where square is not possible (due to irregular geometrical limitations, edges, boundaries, etc.) then, we can adapt rectangular quadrilateral elements, trilateral (triangular), trapezoidal, or polygonal elements. Mainly extreme aspect rations needed to be avoided by reducing the mesh size. The larger the mesh size, the less precise the result. The smaller the mesh size, the higher the number of elements, and the longer the analysis time. Judge the balance, try to keep optimum mesh size. After creating the model in Midas Civil, define domain and sub-domain for calculating wood-armer moment.

B. Element Sectional & Material Properties:

Relevant material and section properties are needed to be defined for slab/crossheads/columns/piles. By using a user-defined/ pre-defined database in Midas Civil material and section properties can be created

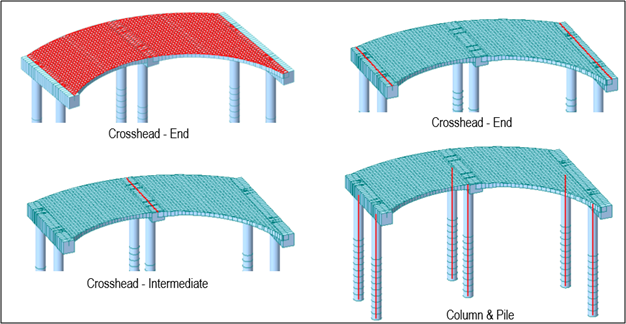
C. Boundaries:

Point spring supports are applied to sections of the pile with the relevant stiffness in all DOFs according to their depth. Different spring constants are based on the soil investigation report and the geotechnical engineer’s recommendations. Shaft friction is not considered. Vertical support provided only by pile end bearing. These stiffness values can be calculated manually and point spring could be defined at each node separately. To avoid this complexity, Midas Civil provides an option to create these point springs along with proper stiffness values automatically by using provided soil data. On the basis of the provide soil data like ground level, soil type, Pile diameter, soil density, earth pressure coefficients, coefficient of Subgrade Reaction(Kh), Internal Friction Angle(phi) & Initial Modulus (k1) the software calculates the corresponding stiffness for the point spring.

Refer to this link to know more about the background calculation of spring stiffness from the soil data.

http://manual.midasuser.com/EN_Common/Civil/895/Start/04_Model/06_Boundaries/Integral_Bridge_Spring_Supports.htm

The connection between the deck and crosshead can be made of the rigid type of elastic links if it needs to be considered as a monolithic connection, otherwise, relevant stiffness can be defined in the elastic link.

D. Loading the bridge:

For the further ultimate load & service load checks, the following loads should be applied.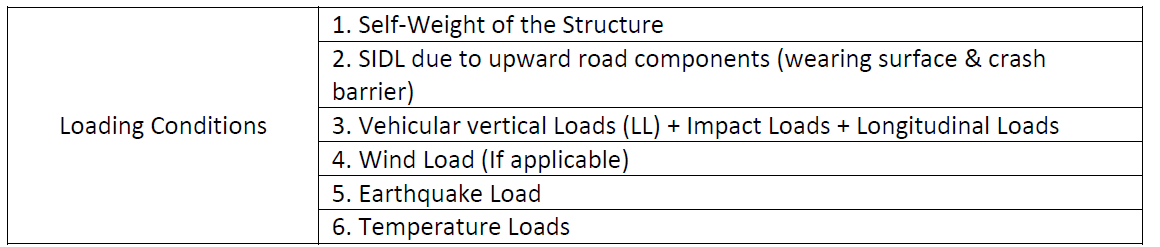

In general Moving Load Analysis becomes the most difficult part of the analysis as the number of cases need to be considered. Moving load analysis in Midas Civil works on the influence line method, in which the program automatically moves the vehicle in the longitudinal direction in the defined lane, even it automatically checks the critical location of the vehicle in the transverse along with the longitudinal direction if “Moving Load Optimization” is defined.

There are notional lanes along with the curved slab and HA & HB vehicle load of BD 37/01 were applied along those lanes. Midas Civil helps to cover variables much easier, e.g. the different distances between the 2 inner axles of an HB vehicle, an HB vehicle straddling between 2 lanes, “loaded length” of HA loading.

To apply a moving load, three features must be defined: Traffic Surface Lanes, Vehicles, and Moving Load Cases.

(1) The Traffic Surface Lane is used to define the location where the vehicle is loaded.

(2) The Vehicle is used to define vehicle data according to the design code.

(3) The Moving Load Case is used to define the number of lanes and the combination factor.

These dummies are needed to make easier the selection of the nodes to be referenced when creating traffic surface lanes. These nodes shall be renumbered to be consistently increasing/decreasing along the traffic load direction.

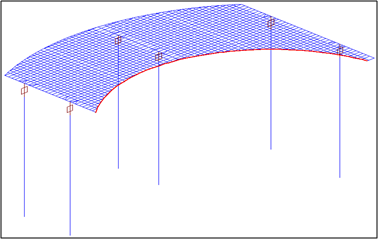
If offset is applied while the dummy is selected, the traffic surface lane is created on the slab. At this time, the location rules vary depending on whether the inner curve or outer curve is selected. The value of offset to the lane is applied in the orthogonal direction of the curved line of the reference edge.

Therefore, if those along the outer curve edge are selected and offset towards to inner curve, some parts of the deck will not be covered and thus will not be loaded with any moving loads.

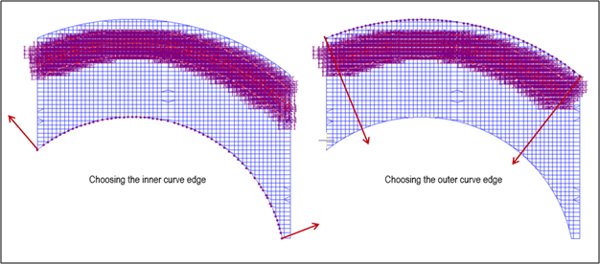
In the moving load case option, a load combination can be automatically created according to the vehicle already defined. At this time, the sub-load case option can be used to select which lane the vehicle can be loaded with the combined condition or independent condition. 

If, instead of “HA & HB (Auto)”, HA and HB vehicles are defined separately, uncheck “Auto Live Load Combination”. In this case, choose the “Independent” option under Sub-Load Cases, and combine the reactions from each traffic load configuration manually using a load combination.

4. Analysis & Results using midas Civil

After performing analysis, several results can be extracted in graphical & tabular format for the further creation of load combinations that are required for design checks.

A. Moving Load Result: 

The envelope results of moving load analysis could be used for load combination. The loading positions and values of the vehicle can be displayed when the maximum result (moment/shear or axial force) occurs in the key element. The loading positions can appear clearly by the function of moving load tracer. 

B. Wood-Armer Moments:

Wood Armer method allows moment triads from plates (Mx, My, Mxy) to be transformed into simple bending moments in two directions (Wood Armer moments) for reinforcement design of plate elements. This is important because the twisting moment Mxy can be significant.

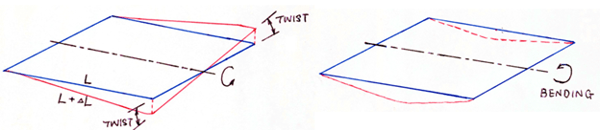
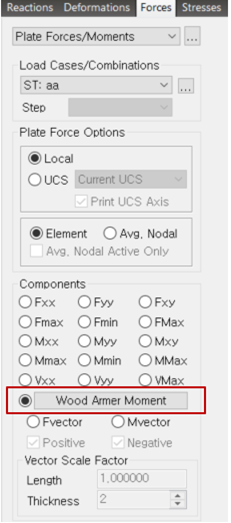
The Wood-armer moments could be obtained at the top and bottom of plates along with both the reinforcement directions. This option could be accessed by clicking on the ‘Wood-Armer Moment’ button as highlighted in the image below.

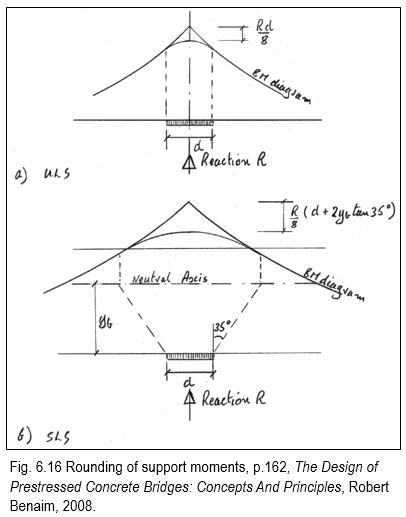
C. Rounding of the Support Moments:

In many occasions, the “peak” hogging moment is greater than the sagging moment. “Peak” hogging moment is calculated assuming “stick” support, which is not the exact case. The load above the support is “counter-acted” by the support reaction R distributed over d (or d + yb tan 35°). Simply-supported mechanism assumed for moment reduction. The reduction is limited to 10 % of peak hogging moment.

“The reduction of the moment due to the physical width of the bearing is purely mechanical, and is effective both at working and ultimate loads. The spread through the height of the beam is an elastic effect, and should not be used at the ULS”. – Robert Benaim

5. Design and Optimization

Below checks need to be performed as per relevant standard:

• ULS Bending Moment Capacity
• ULS Shear and Torsion Capacity
• SLS Stress Check
• Crack Width Control & Deflection Check
• Punching Shear Check

As Self-weight is a load much more significant in solid slab deck than other more advanced types of deck. Cutting down self-weight could give obvious savings to materials, labors, times, which all translate well into savings in cost. But, how much to cut down? For this several trials had been carried out before arriving at the final optimized design. In the trial models, several sections have to check to find the optimized size. The following picture shows the final design after optimization. A reduction of about 25 % was achieved by reducing the depth of the slab in the middle which further reduce the material requirement for the substructure and the foundation.

Watch the full webinar video