C. Eigenvalue Analysis
Structures have natural vibration characteristics depending on their shape, material, and boundary conditions. Natural vibration characteristics refers to a free vibration state that does not receive any external forces. The analysis method to find these characteristics is called mode analysis, eigenvalue analysis, or free vibration analysis. Through the eigenvalue analysis, it is possible to know the natural frequency of the structure and the corresponding eigen-mode. The natural frequency represents the degree of how quickly it repeats per unit time, and the eigen-mode refers to a shape that can be freely deformed under a given constraint.
The natural vibration characteristics of the structure can be obtained from the undamped free vibration, which is a state that is not affected by external forces. Since it is an undamped free vibration, a dynamic equilibrium equation in which the damping matrix and external force are zero can be created. Furthermore, the natural frequency and eigen-mode can be calculated by assuming the displacement vector u(t) as the product of the displacement shape function and the time function. The MDOF system can be calculated in the same way as the SDOF system, except that the stiffness and mass are in matrix form.
The smallest natural frequency (longest natural vibration period) is referred to as the fundamental natural frequency of a structure, and is used as an important measurement of the dynamic characteristics of the structure. By knowing the natural frequency, corresponding mode shapes (free vibration mode, vibration mode or mode) can be obtained. The free vibration mode, which is the main problem of eigenvalues, represents only its shape as a combination of relative values, and assumes an absolute size as an arbitrary value. Therefore, since it is inconvenient to use the amplitude of the mode as an arbitrary value in numerical analysis, determining the amplitude of the mode shape according to a certain criterion is referred to as the normalization of the mode shape, and the mode obtained is called the normal mode.
The degree of freedom increases indefinitely as the analysis model of the structure becomes realistic. Since modes are created as much as the number of degrees of freedom the structure has, a situation arises in which a system of differential equations having as many unknowns as the number of degrees of freedom must be solved. Therefore, an appropriate degree of freedom should be selected and analyzed for efficient dynamic analysis, and one of the effective ways to reduce the degree of freedom is the mode superposition method using the eigenvector of the structure.
As mentioned above, accurately modeling the stiffness matrix in a structural analysis model that is similar to the actual behavior results in a greater degree of freedom. The mode superposition method does not consider all of these degrees of freedom in the dynamic analysis, but is a method of increasing the efficiency by including only the eigenvector or Ritz Vector, which has a major effect on the dynamic analysis. The figure below shows the basic concept of the mode superposition method, and shows that the deformed shape of a structure with multiple degrees of freedom can be expressed with only one representative mode.


/11.%20Dynamic%20Analysis/Figure/Dynamic%20Analysis_figure_(1)-2-1.jpg)
/11.%20Dynamic%20Analysis/Figure/Dynamic%20Analysis_figure_(2)-1-1.jpg)
/11.%20Dynamic%20Analysis/Figure/Dynamic%20Analysis_figure_(3)-1-1-1.jpeg)
/11.%20Dynamic%20Analysis/Figure/Dynamic%20Analysis_figure_(4)-1-1-1.jpeg)
/11.%20Dynamic%20Analysis/Figure/Dynamic%20Analysis_figure_(5)-1-1.jpeg)
/11.%20Dynamic%20Analysis/Figure/Dynamic%20Analysis_figure_(6)-1-1.jpg)
/11.%20Dynamic%20Analysis/Figure/Dynamic%20Analysis_figure_(7)-1-1.jpeg)
/11.%20Dynamic%20Analysis/Figure/Dynamic%20Analysis_figure_(8)-1-1-1.jpg)
/11.%20Dynamic%20Analysis/Figure/Dynamic%20Analysis_figure_(9)-1-1.jpeg)
/11.%20Dynamic%20Analysis/Figure/Dynamic%20Analysis_figure_(10)-1-1.jpeg)
/11.%20Dynamic%20Analysis/Figure/Dynamic%20Analysis_figure_(11)-1-1.jpg)
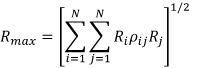
/11.%20Dynamic%20Analysis/Figure/Dynamic%20Analysis_figure_(12)-1-1.jpg)
/11.%20Dynamic%20Analysis/Figure/Dynamic%20Analysis_figure_(13)-2.jpg)