A. Introduction:

Differential shrinkage is a phenomenon that occurs in composite sections, which are made up of different materials or different grades of concrete, as the different materials will experience a different rate of shrinkage (i.e., PSC composite I Girder). In this article, we will focus on differential shrinkage due to the different time-dependent effects for the composite section consisting of the same material with different grades of concrete for the deck slab and the girder. Differential shrinkage is an important concept to consider when designing composite sections even when the same material is used for both the girder and deck, the age difference will cause the differential shrinkage effects. This will induce different time-dependent effects on both since both the parts are integrally connected internal stress will be generated to reduce the differential effect.

• In composite beams, the shrinkage strain of the deck slab and precast beam differ after the beam is made composite. Some shrinkage has already taken place in the precast beam till the shrinkage of the deck starts.
• Additional stresses are set up by differential shrinkage.
• It must be included at the serviceability limit state in composite beams.
• This relative shrinkage will compress the top of the precast beam (causing axial force and sagging moment in it while generating tension in the deck slab itself).

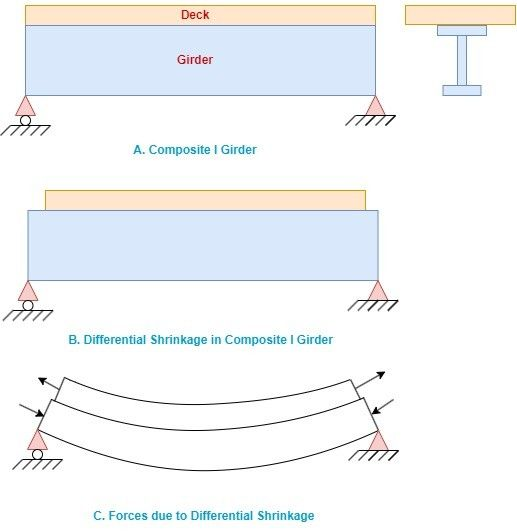
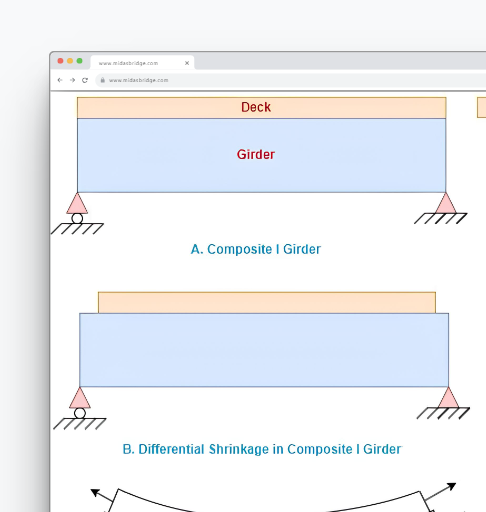
B. Differential Shrinkage in Composite Section

A composite section refers to a structural member that is made up of different materials or the same material with different grades of concrete that are bonded together to act as an integral section. Creating a composite section is to utilize each material’s advantages, such as strength, stiffness, and durability, to create a stronger and more efficient structural member. These sections are used widely nowadays, in general, in construction sequence the precast beam is cast before the deck slab and the beam will have undergone a significant part of its total shrinkage by the time the deck slab is cast, so the deck slab will shrink by a relatively greater amount. The relative shrinkage will result in tensile stress in the deck slab and compressive stress in the top fiber of the girder section. There are several methods available for analyzing the effects of differential shrinkage, as per EN 1992 the differential shrinkage can be estimated from 2-2/ clause 3.1.4 if the approximated age of the beam at casting is known.

Designer Guide to EN 1992-2, Annex K 4.2

Where εsh, beam (∞) is the total shrinkage strain of the precast beam, εsh, slab (∞)  is the total shrinkage strain of the slab, and εsh, beam (t1) **is the shrinkage strain of the precast beam before casting the slab.

B.1 Differential Shrinkage as per EN 1992-1-1 (2004)

In MIDAS CIVIL, The shrinkage effects can be categorized in two ways:

• Primary effects: Shrinkage Primary
• Secondary effects: Shrinkage Secondary

The shrinkage primary effects refer to the deformation and forces required to cause the shrinkage strain and can be calculated based on the formula given in various design codes. While the shrinkage secondary refers to effects caused by shrinkage strain in indeterminate structure.

As per EN 1992-1-1 (2004), “The total shrinkage strain is composed of two components. The drying shrinkage strain (εcd) and the autogenous shrinkage strain (εca). The drying shrinkage strain develops slowly since it is a function of the migration of water through the hardened concrete. Drying shrinkage is associated with the loss of water from the concrete section and therefore depends on the relative humidity, the effective section, and the concrete composition. Drying shrinkage occurs more slowly and continues for several years after the concrete is cast. The autogenous shrinkage strain develops during the hardening of the concrete and occurs for the first few days after casting. Autogenous shrinkage occurs during hydration and hardening of the concrete without loss of moisture and total strain depends only on the concrete strength. Autogenous shrinkage is a linear function of the concrete strength, it should be considered specifically when new concrete is cast against hardened concrete. The total shrinkage strain (εcs) can be calculated using the following equation.

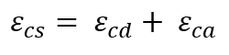
EN 1992-1-1 (2004), [3.8]

The final value of the drying shrinkage strain, εcd (∞) is equal to kh·εcd(0). εcd(0)  can be calculated using the formula given in Annex B

The basic drying shrinkage strain εcd(0) is calculated from.

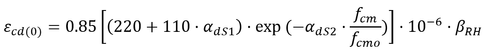
EN 1992-1-1 (2004), [B.11]

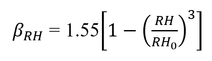
EN 1992-1-1 (2004), [B.12]

where,
fcm is the mean compressive strength (Mpa)
fcmo is 10 Mpa
αds1 is a coefficient that depends on the type of cement
= 3 for cement Class S
= 4 for cement Class N
= 6 for cement Class R
αds2 is a coefficient that depends on the type of cement
= 0.13 for cement Class S
= 0.12 for cement Class N
= 0.11 for cement Class R
RH is the relative humidity (%)
RH0 is 100%