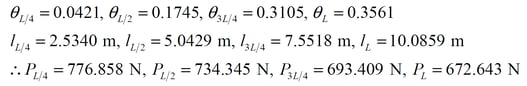Get Started midas Civil
Featured blog of this week
With the advent of the IT era in the 21st century, information that was previously unavailable in the engineering market has become possible. Engineering simulation using a computer program is one of them, and it is currently used in most engineering industries.
In order to perform a correct structural analysis simulation using such a computer analysis program, it is necessary to compare and verify the contents of engineering theory and the results calculated by the program. It is an essential process in industries such as construction and transportation, which are directly related to human safety.
In this post, we will compare the theoretical contents to the analysis results in a structural analysis program about the prestressed concrete equilibrium equation and the prestressed tendon loss.
PSC bridge is a bridge type that secures the stability of the structure by introducing artificial deformation and stress using tendon to the concrete member. The stress introduction by tendon depends on the tendon shape and tension. The shape of the tendon is defined as the distance from the neutral axis of the member. If the neutral axis changes for each construction stage, such as the composite section in the construction stage, this should be appropriately reflected.
Tension can be divided into immediate losses, such as friction or anchorage losses, and time-dependent losses that occur as the construction stage progresses, such as elasticity change or relaxation. Such tendon losses must be properly reflected in the analysis.
1. Verification of Equivalent Tendon Force
Assuming that there is no Tendon Losses, the equivalent tendon force is calculated as follows.
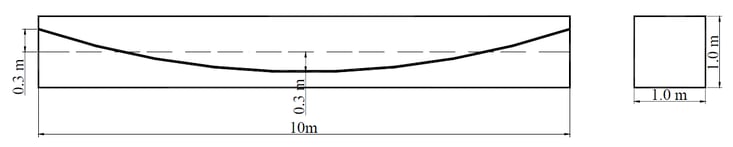
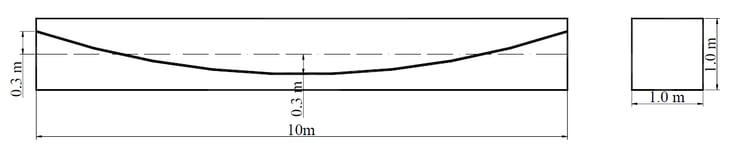
Material and section properties are following:
|
Modulus of Elasticity (Conc), |
Ec |
10,000 |
|
Modulus of Elasticity (Steel) |
Es |
150,000 |
|
Area of Steel |
Ast |
0.01 |
|
Yield Stress |
Fy |
100,000 |
|
Diameter of Duct |
dduct |
0.04 m |
|
Tensile Stress |
fso |
80,000 |
|
Eccentricity |
ei |
0.3 m |
|
Span length |
L |
10 m |
→ Theoretical approach method and calculation results
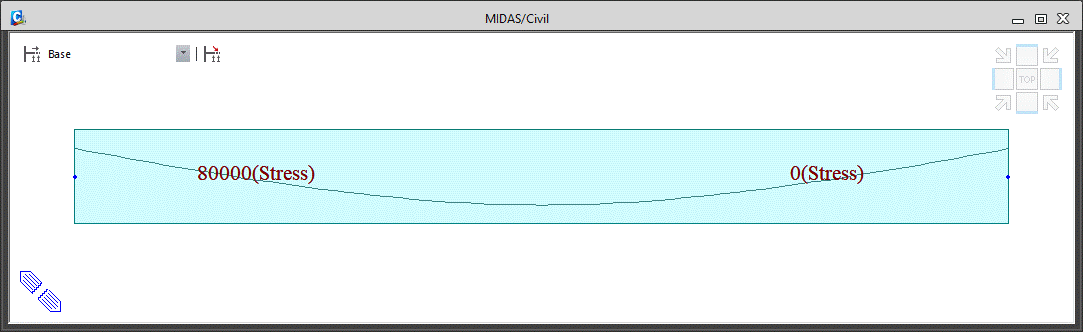
i. Calculate the tension force at each at each L/4 position for one beam, and calculation the equivalent tendon force acting on the beam. Ignoring the tendon losses, the tension at each L/4 position of the beam is as follows.
ii. Here, the arrangement of the tendons in each section is assumed to be linear.
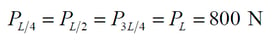
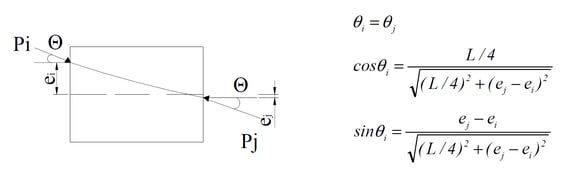
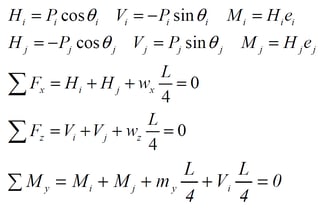
iii. The neutral axis moves because the area of the tension member and the duct is calculated as a transformed cross section. Where, each position is described as e0=i, e1=1/4, e2=2/4.
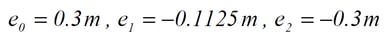
After the change of the neutral axis by the effective section,
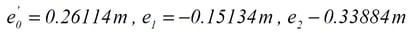
iv. Where Pi=Pj and ei=ej,
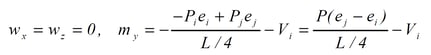
Therefore, the equivalent tendon force acting on each section is shown in the below figure.
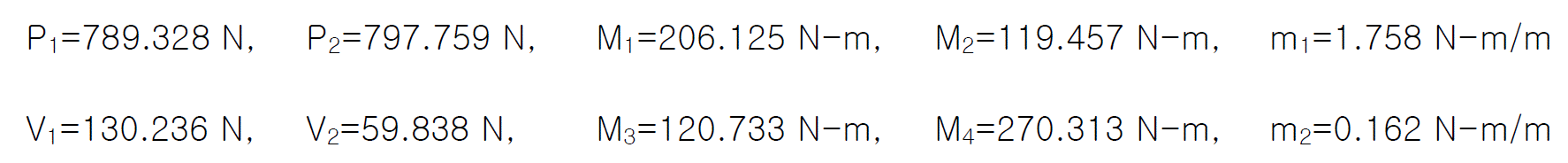
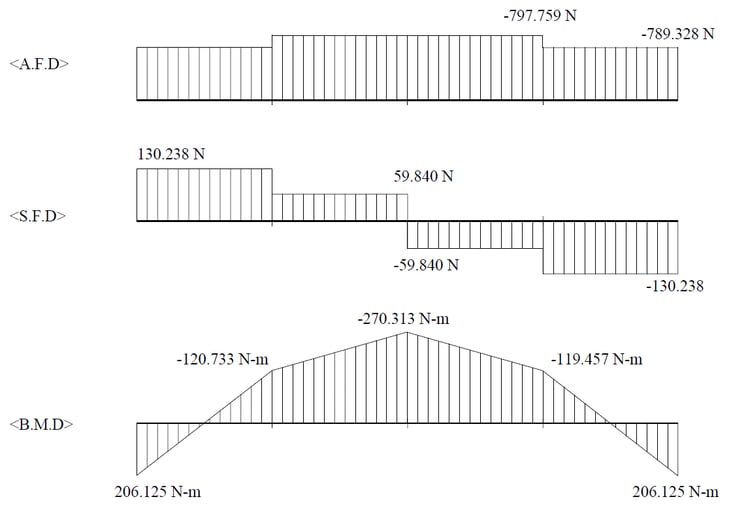
v. Member force diagram
→ Modelling and structural analysis result by midas Civil
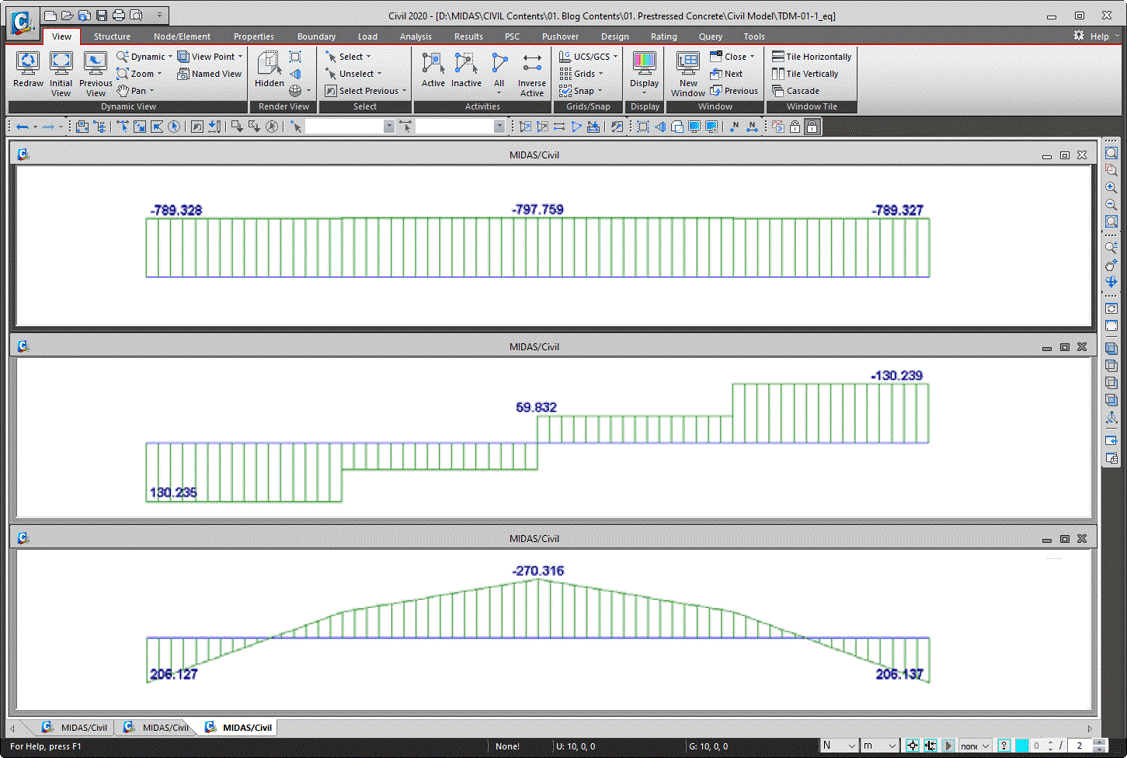
i. Input Model
ii. Input Load
iii. Analysis Results
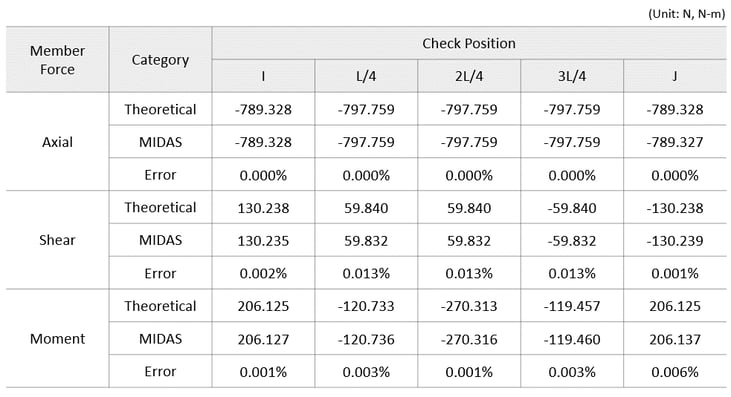
→ Comparison of theoretical results and analysis results using midas Civil
2. Tendon Losses due to Friction, Anchorage Slip, and Relaxation
Material and section properties are following:
|
Modulus of Elasticity (Conc) |
Ec |
10,000 |
|
Anchorage slip |
Lslip |
0.05 m |
|
Modulus of Elasticity (Steel) |
Es |
150,000 |
|
Relaxation coefficient |
Crelax |
45 |
|
Area of Steel |
Ast |
0.01 |
|
Curvature friction factor |
μ |
0.3 |
|
Yield Stress |
Fy |
100,000 |
|
Wobble friction factor |
k |
0.0066/m |
|
Diameter of Duct |
dduct |
0.04 m |
|
|
t1 |
100 day |
|
Tensile Stress |
fso |
80,000 |
|
|
||
|
Eccentricity |
ei |
0.3 m |
|
|
||
|
|
ej |
0.3 m |
|
|
||
|
Span length |
L |
10 m |
|
|
||
→Theoretical approach method and calculation results
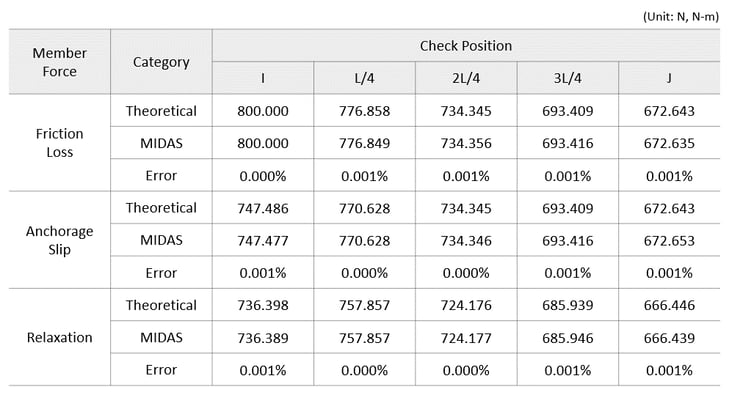
i) Loss due to friction
The tension at each L/4 point is as follows.
ii) Loss due to anchorage slip
Let the length of the tendon subject to reverse friction be set, calculate the tendon loss due to settlement activity based on where this length is in any of the four sections.
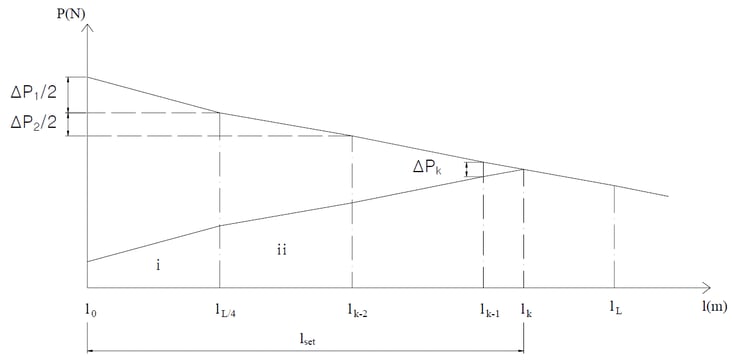Tendon loss graph by anchorage slip
(a) Section I
(b) Section ii
The rest remains, PL/2, P3L/4, PL unchanged.
iii) Loss due to relaxation
Loss due to relaxation is calculated as follows.
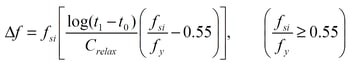Here, fsi is the stress before loss due to relaxation occurs, and t is the elapsed time (hr). Crelax is relaxation coefficient (45 in this example), and fy (100,000 N/m2) is yield stress.
Therefore, the tension force considering the loss due to relaxation at each point is as follows.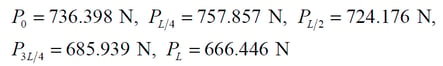
→ Modelling and structural analysis result by midas Civil
i) Input Model
ii) Input Load
iii) Analysis Results
(a) Loss due to friction
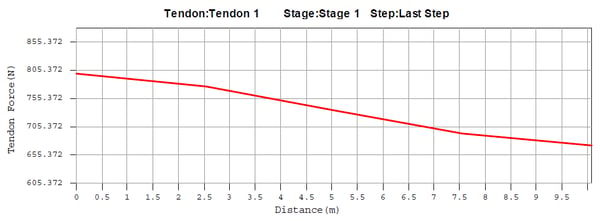
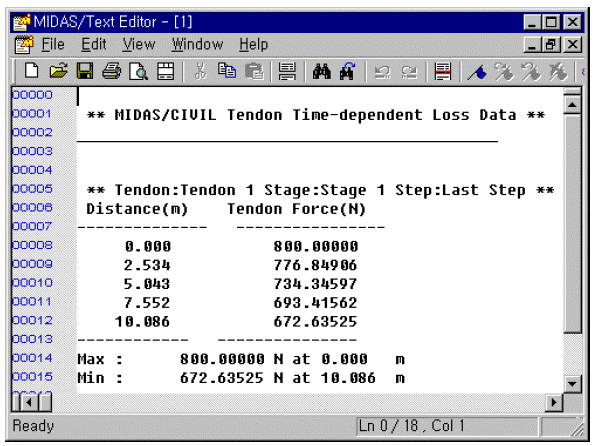
(b) Loss due to anchorage slip
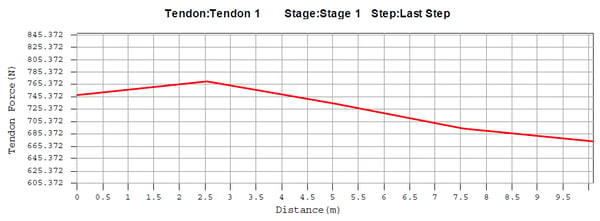
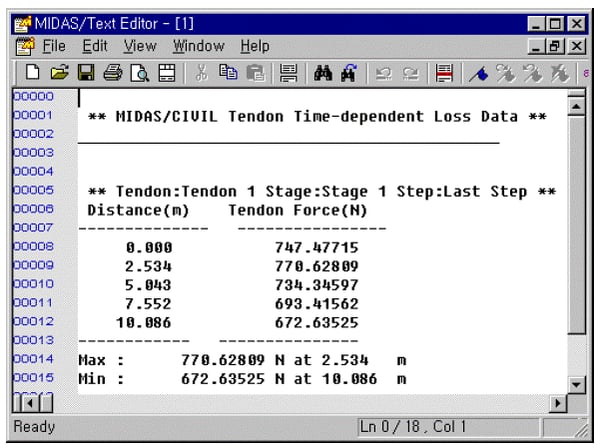
(c) Loss due to relaxation
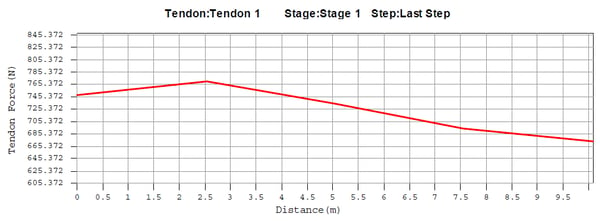
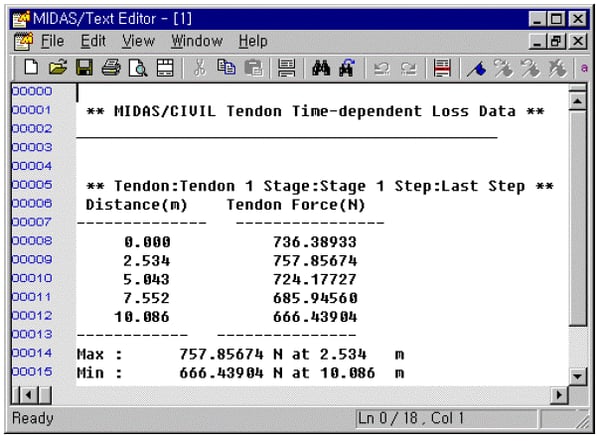
→ Comparison of theoretical results and analysis results using midas Civil
