Get Started midas Civil
Featured blog of this week
📢 To check the entire series, click here
A. Damping Method
1. Modal & Direct Integration Analysis Method
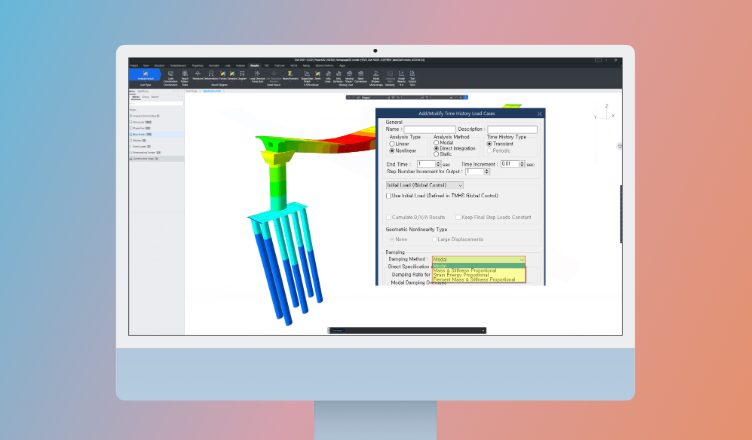
In this section, we will discuss the damping method applied to Nonlinear Boundary Time History Analysis.
There are four types of damping methods.
- Modal,
- Mass & Stiffness Proportional,
- Strain Energy Proportional,
- Element Mass & Stiffness Proportional
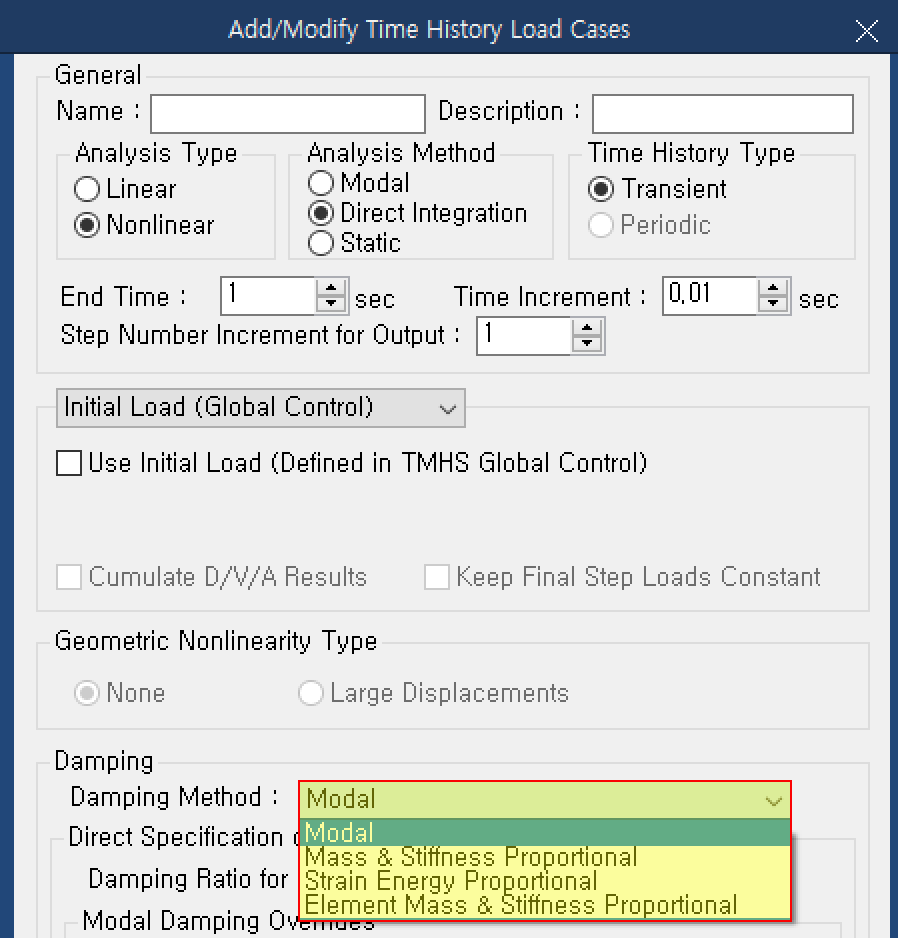
Time History Load Cases - Damping Method
The four damping methods are categorized for analysis purposes as follows.
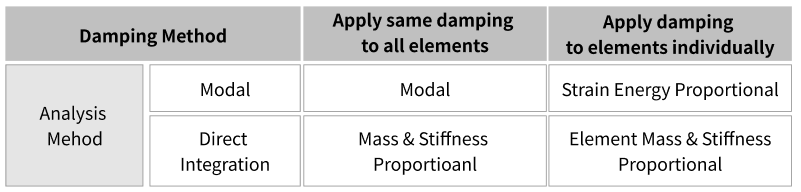
The method of applying damping varies depending on whether you want to apply the same damping to all elements of the structure or not.
The options you choose also depend on whether you use the Modal or Direct Integration methods. The two methods differ in how they account for damping, which can lead to much longer analysis times depending on the selected damping method.
Depending on the analysis method, the recommended damping method is as follows
- For the Modal method, the damping is usually applied as "Modal".
- For direct integration, the damping is generally set to "Mass & Stiffness Proportional".
2. Mass & Stiffness Proportional method
The Mass & Stiffness Proportional method is Rayleigh Damping, which assumes that the damping matrix can be constructed as a linear sum of the mass and stiffness matrices, expressed by the equation below.
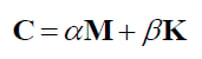
Here, a and b are the damping coefficients, which can be represented by the natural frequency (w) and damping ratio (h) of the two modes.
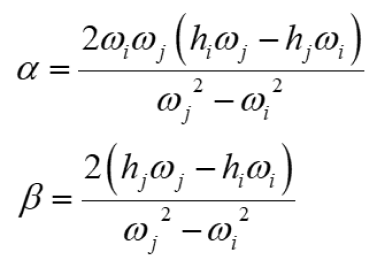
I n MIDAS CIVIL, enter the natural frequency (or period) and damping ratio (typically 0.05) for the two modes.
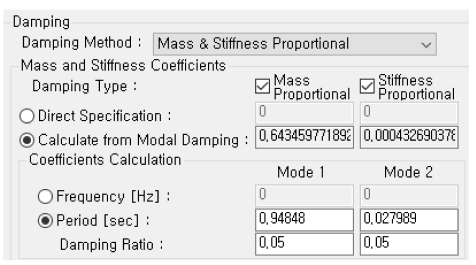
A common question we get is what values should be entered for Mode 1 and Mode 2. (Is it enough to enter the period values for Mode 1 and Mode 2, or what period values should be entered?)
Let's take a look at a quick overview of Rayleigh Damping to get a better understanding.
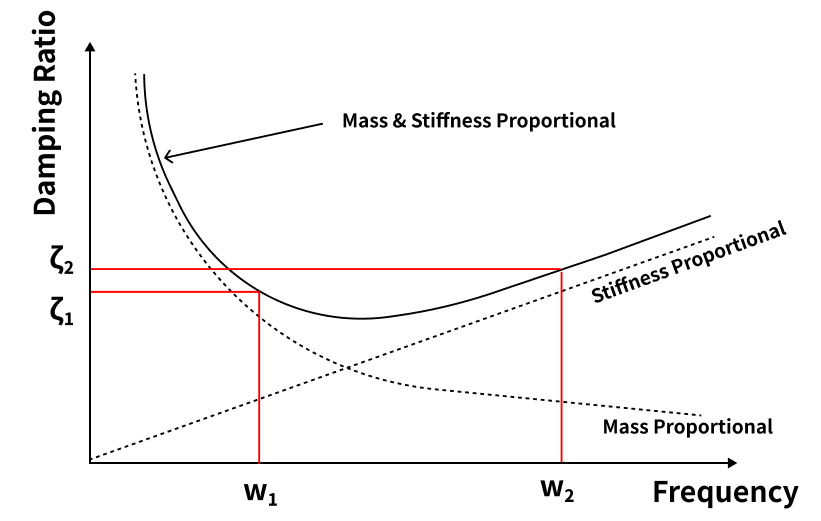
The graph above is for Rayleigh Damping (Mass - Stiffness Proportional Damping).
With two natural frequencies (or periods) and a damping ratio, the coefficients a and b can be calculated, and thus the damping ratio at any frequency can be calculated.
We typically apply a damping ratio of 0.05. However, the determination of two natural frequencies (W1 and W2) with a damping ratio of 0.05 requires engineering judgment.
