📢 To check the entire series, click here
- Non-linear Temperature Gradient Part 1. AASHTO LRFD
- Non-linear Temperature Gradient Part 2. BS Code & Eurocode
- Non-linear Temperature Gradient Part 3. Effects on Beams
- Non-linear Temperature Gradient Part 4. Effects on Bridges
Nonlinear Temperature Effects on Beams
(1) Basic Concept
Through Part 1 & 2, we looked at how the temperature gradient load of a bridge is calculated based on the design criteria. Now, let's examine how the calculated load affects the bridge deck.
Temperature load will cause deformation in members, and in the case of members with free boundary conditions, no stress occurs due to temperature load.
Based on the beam theory, when a cross-section is remain on a plane, temperature load deformation occurs in axial deformation and bending deformation.
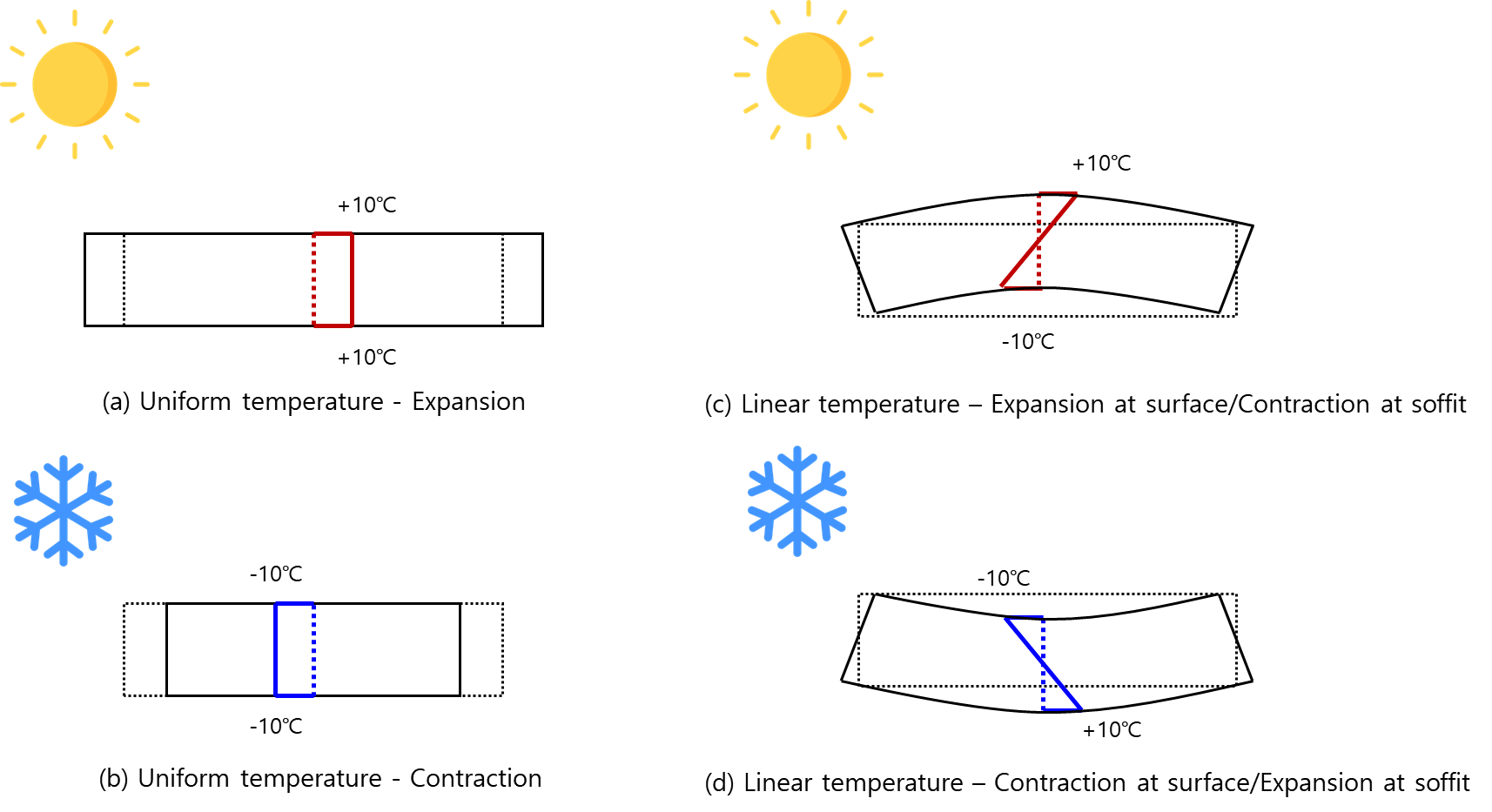
Figure1. Deformation of a beam due to temperature load
When both ends of a beam are restrained and subjected to temperature load, the following stresses are generated:
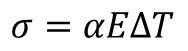
Figure2.
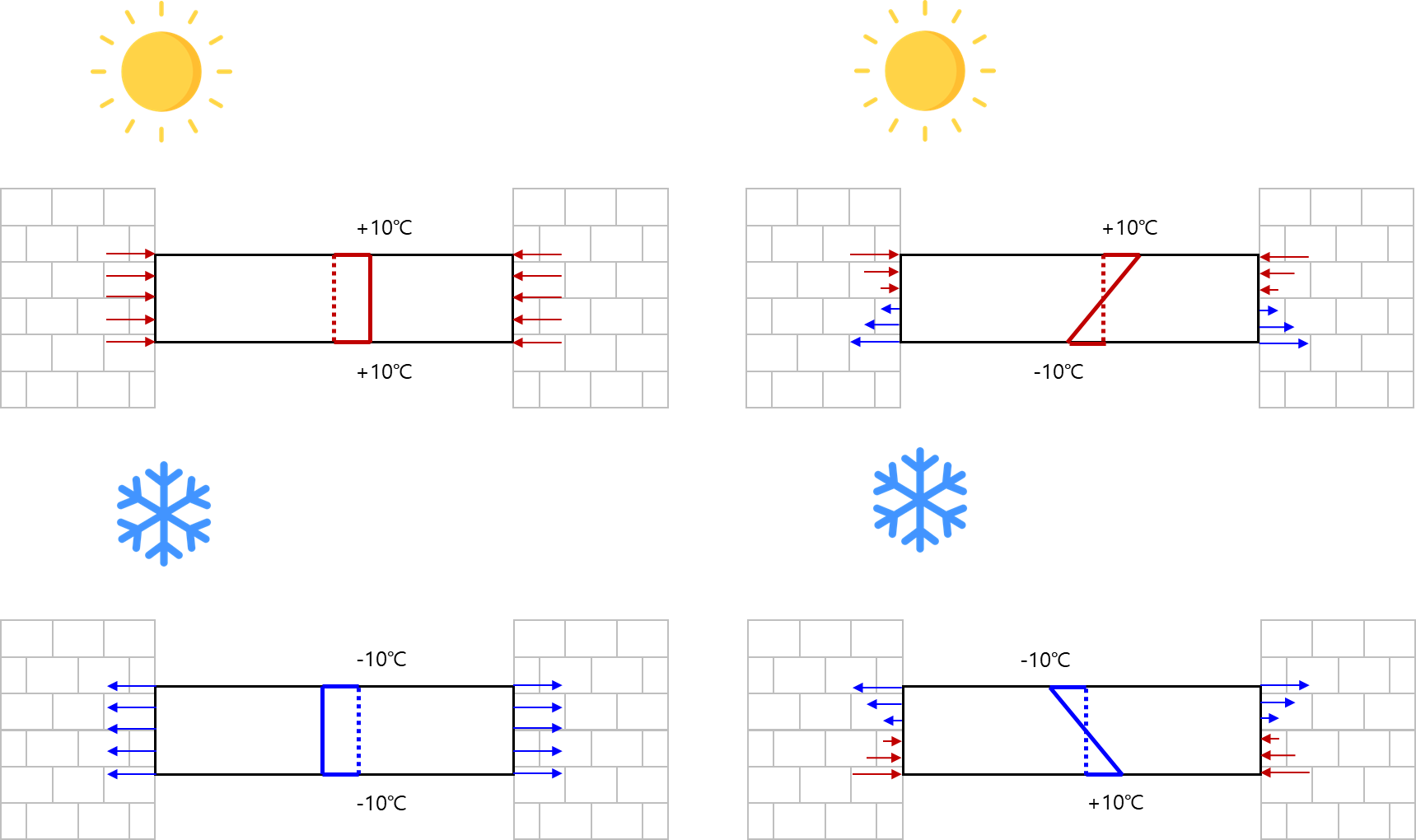
Figure3. Effects on constrained beams
Applying the above concept to non-linear temperature loads, even in a simply supported beam where all restraints are released, residual stress (self-equilibrating eigen stress) occurs in the beam. This can be seen as stress to maintain the equilibrium state of the member according to beam theory.
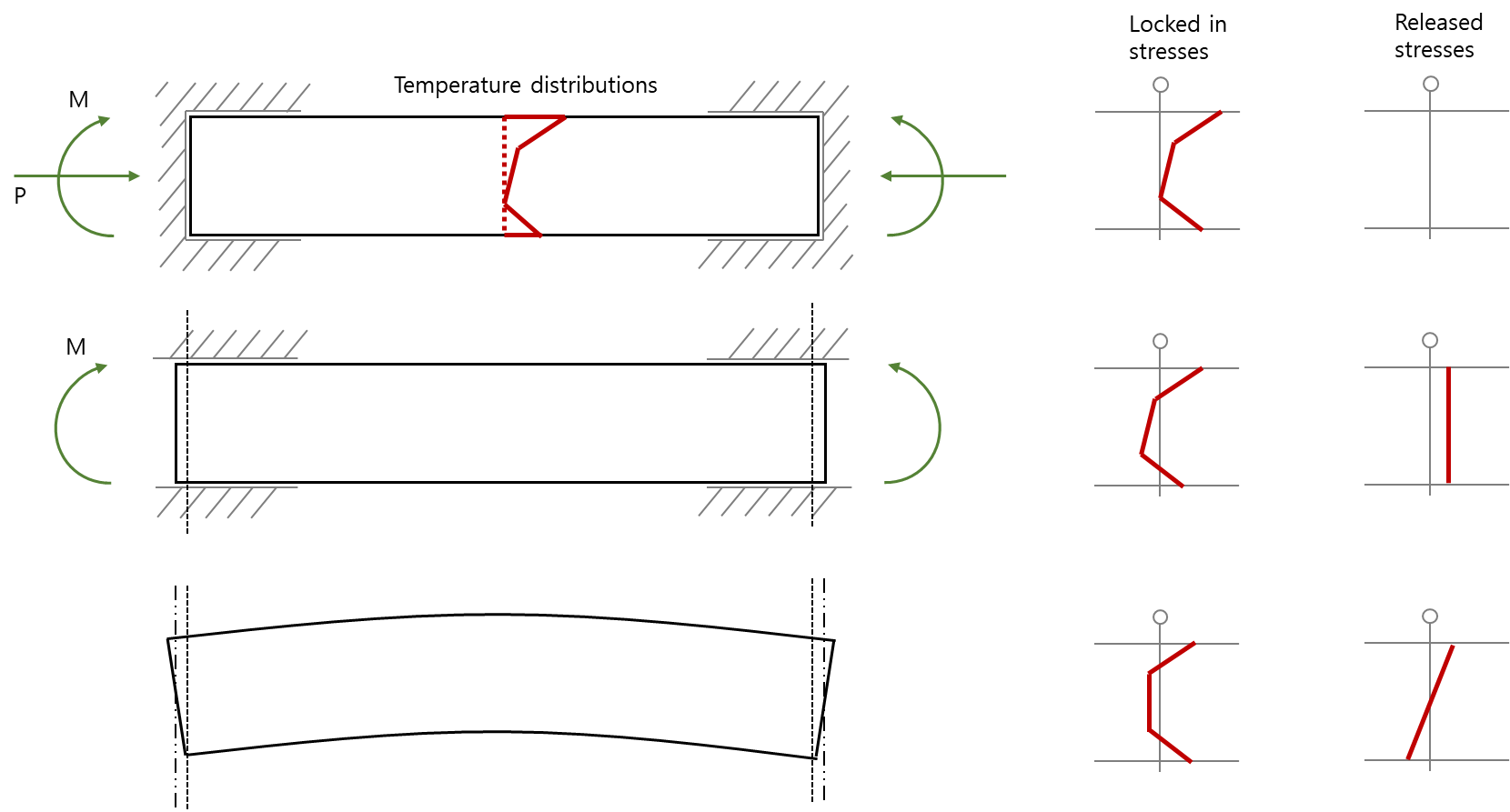
Figure4. Variation in stress for each stage
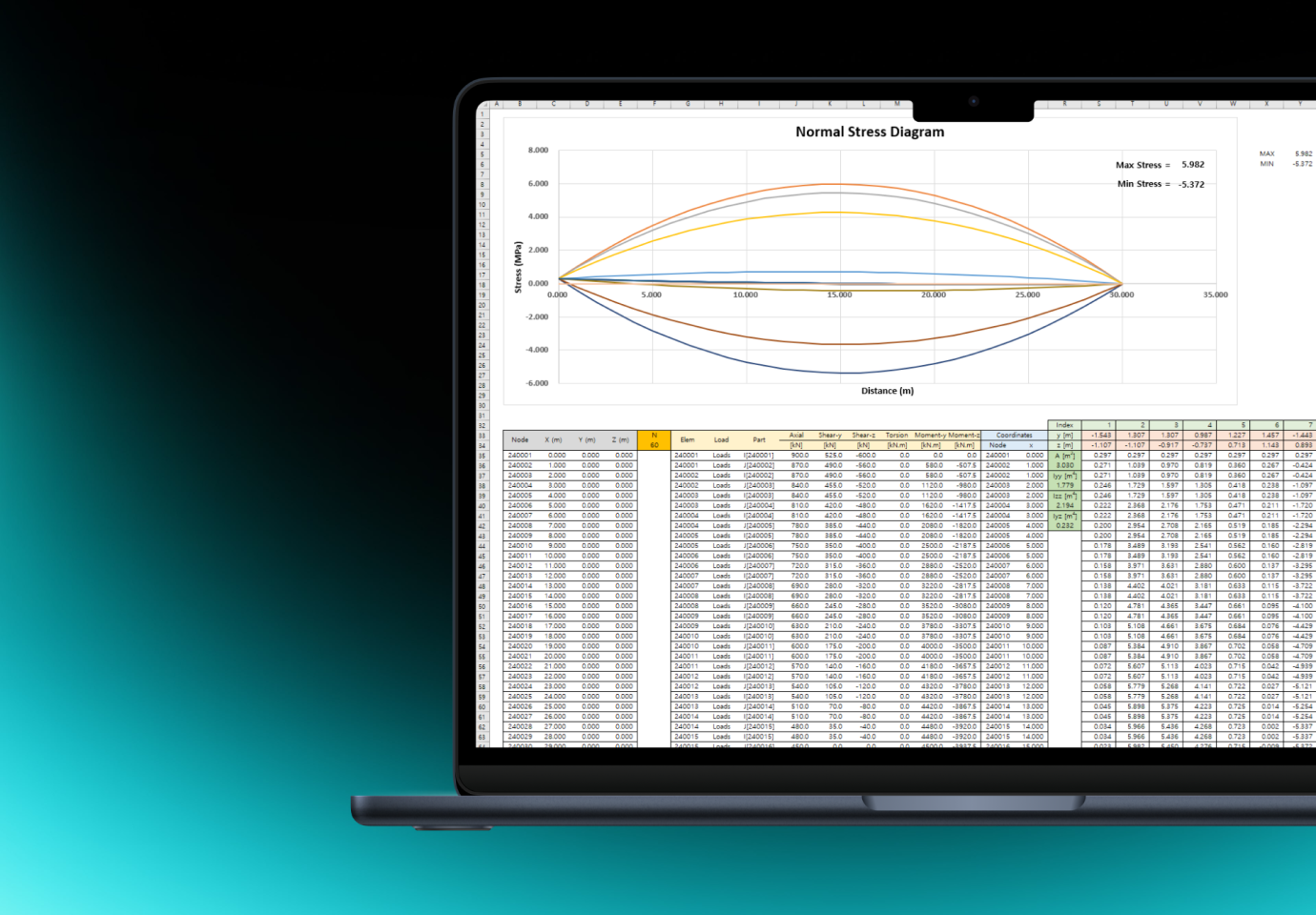
Let's consider the below example to check how residual stress in a simply supported beam is calculated.
(2) Example
Let's assume a beam with a length of L, a width of 1.2m, and a height of 1.5m is subjected to the following non-linear temperature load:
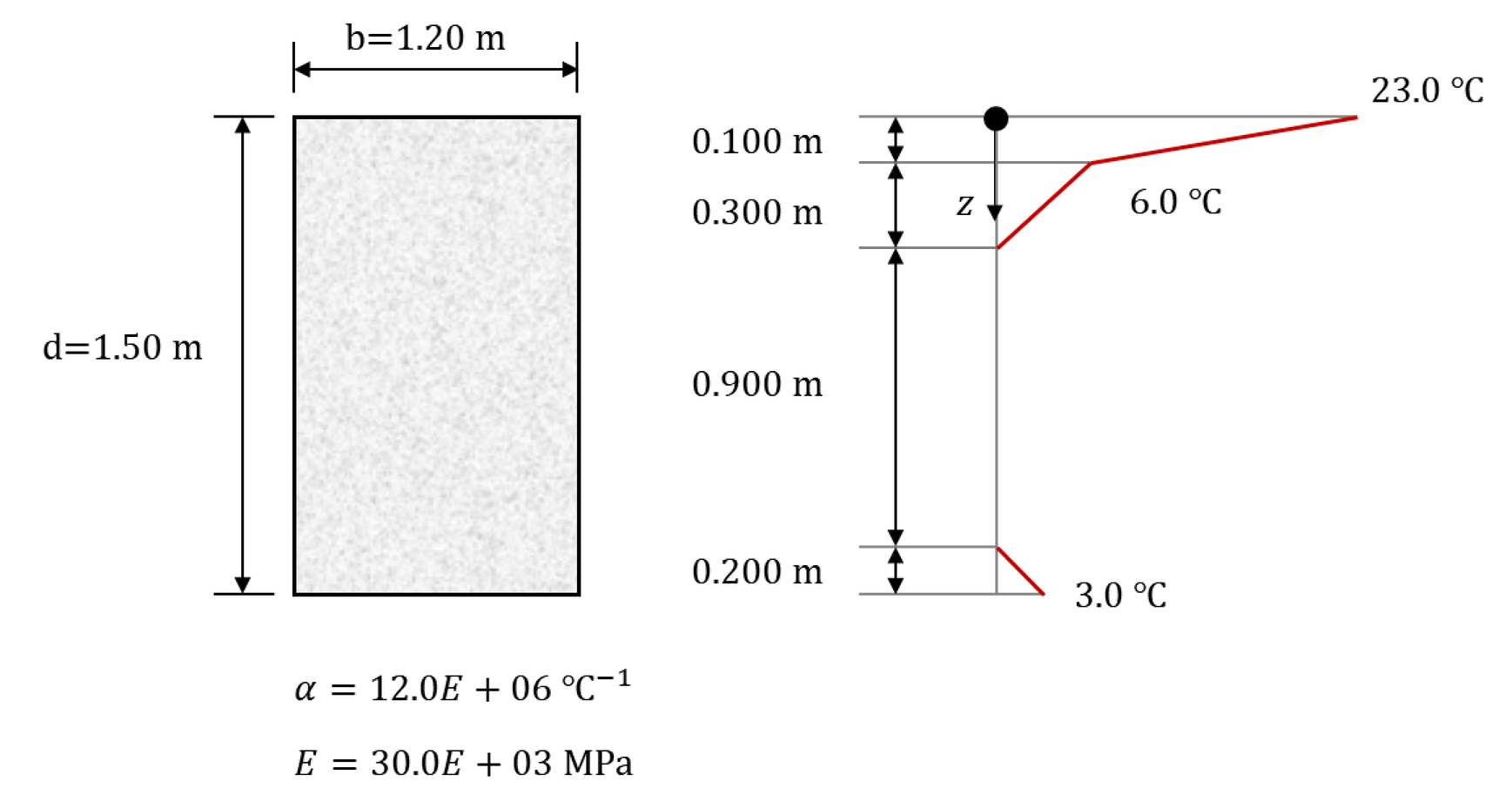
Figure5. Example Cross Section Details
When both ends are restrained, the stress produced in the cross-section is as follows:
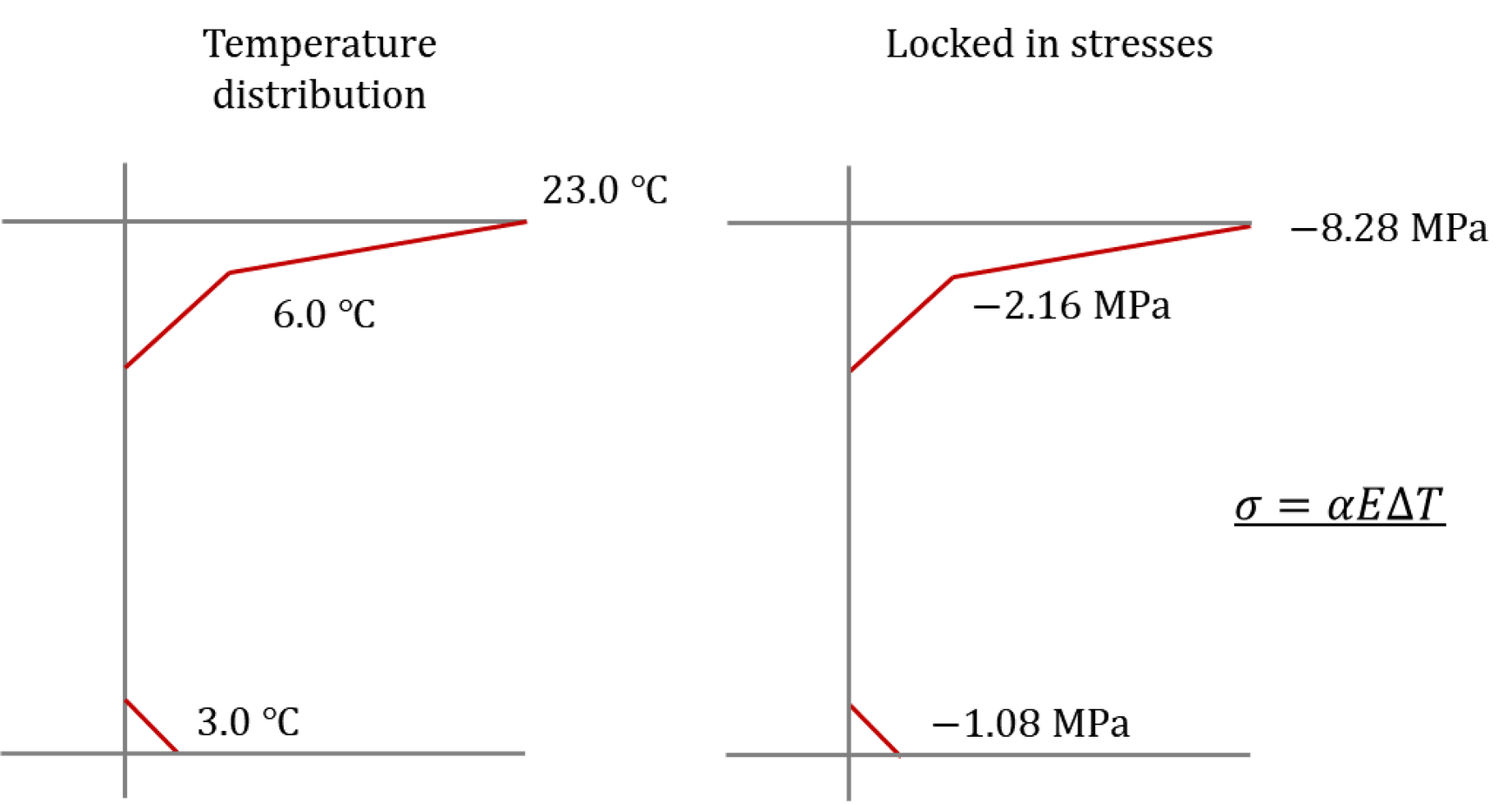
Figure6. Restraint stress due to temperature loading
First, let's calculate the effect of axial restraint.
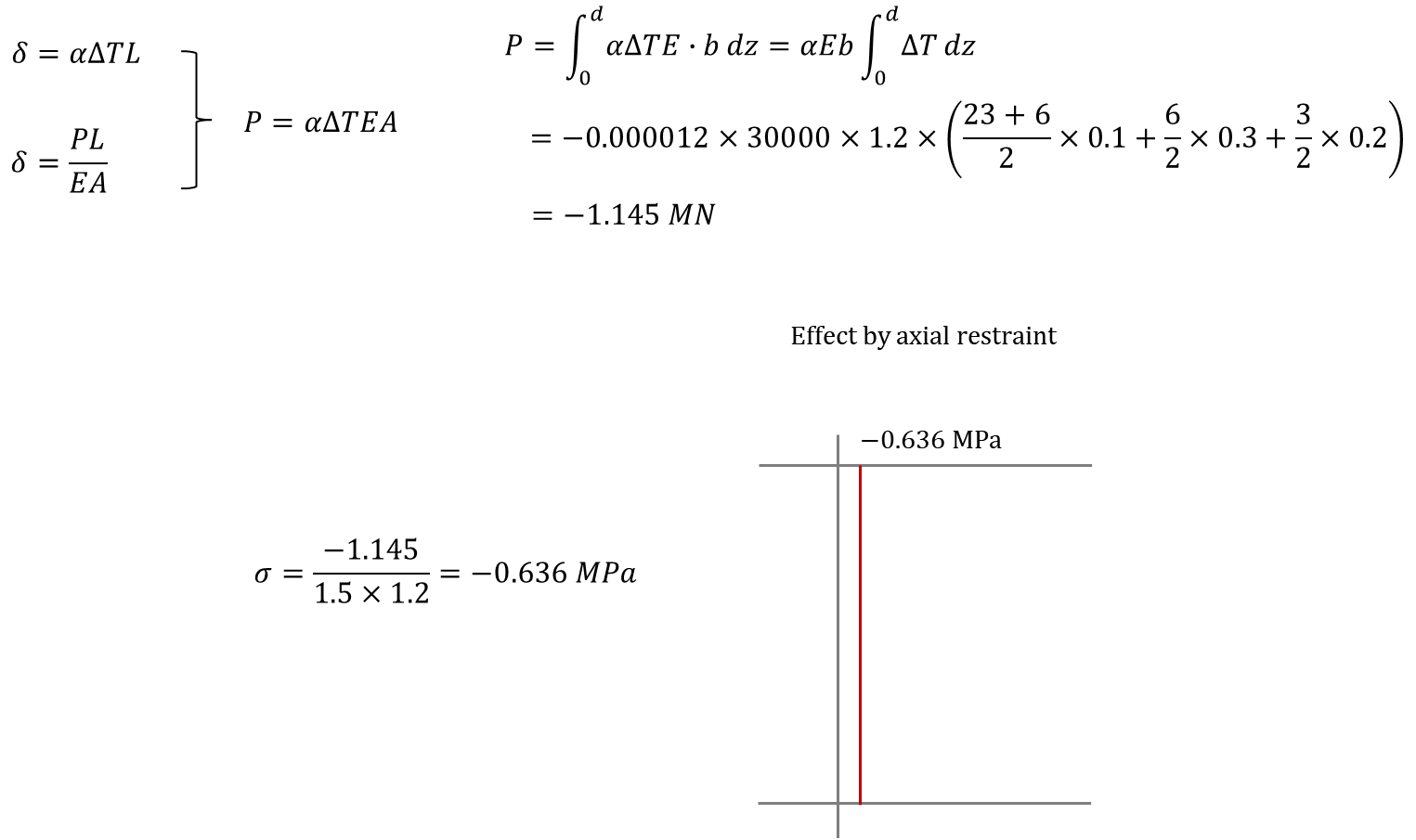
Figure7. Effect of axial restraint
Secondly, when we calculate the effect of bending restraint, we can obtain the following results:
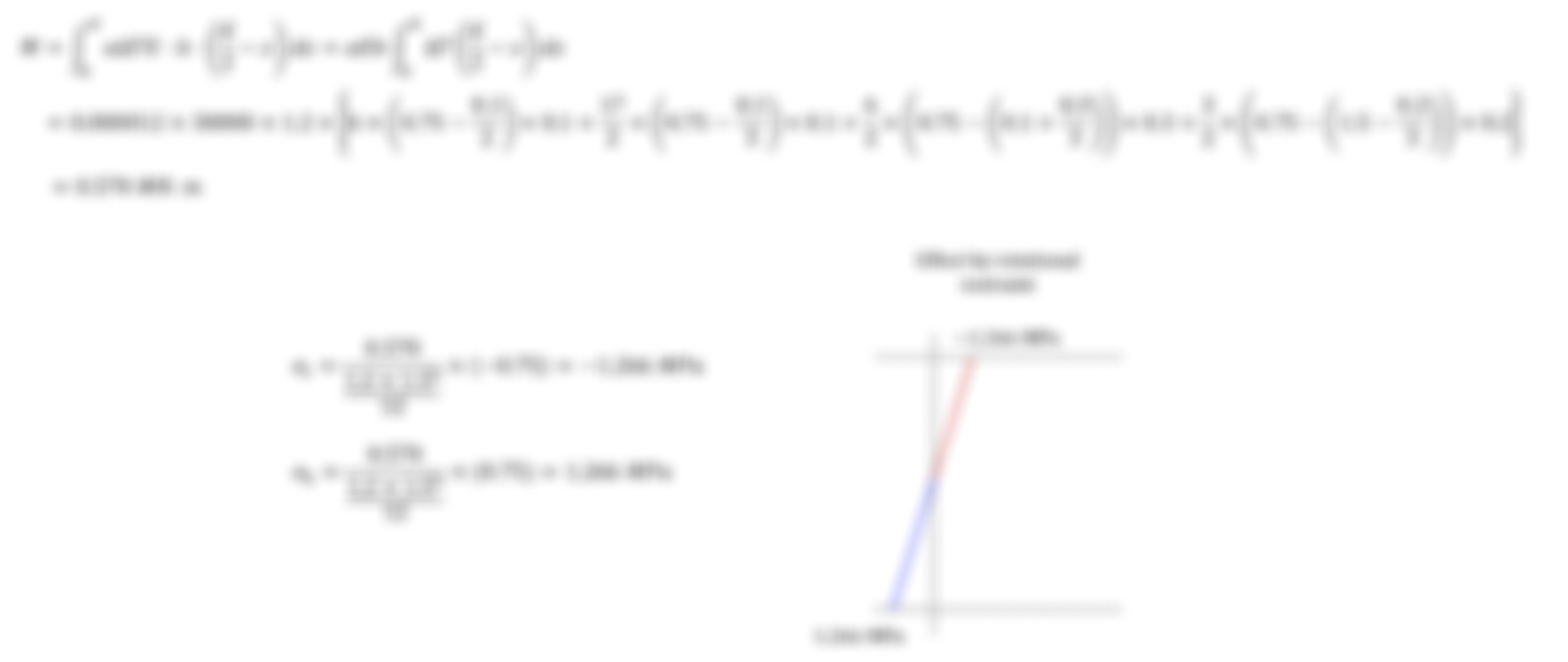
(3) Validation of the example
(4) Conclusion
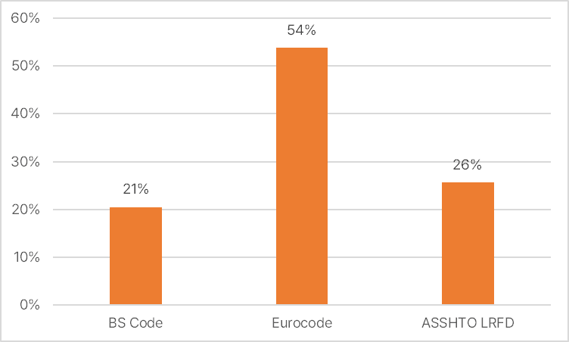
🗳️ Quick Poll Result!
Thank you for participating in the vote! 🗳️ Here are the results. We'll be back with more exciting data and meaningful analysis in the future. Thanks to everyone who took part! 🙏✨
 Get Started midas Civil
Get Started midas Civil
 Featured blog of this week
Featured blog of this week