Get Started midas Civil
Featured blog of this week
📢 To check the entire series, click here
- Green's Theorem Part 1: A Step-by-Step Guide to Calculating Section Properties in Structural Design
- Green's Theorem Part 2: Calculating Normal Stress for Asymmetric Cross-Sections
👉🏻 Check out the Free Download Excel Calculation Sheet
1. Green's theorem
Generally, the theory of section properties is covered in part of Statics or Mechanics of Materials. However, it is widely used in almost all fields, not only in solid mechanics but also in structural dynamics and other areas. If you are an engineer, you will know how important and frequently section properties are used in structural design.
This content is not about the actual theoretical background of section properties but about the technical skills for calculating section properties. One may wonder why "Green's theorem" is used to calculate section properties. However, we will share our know-how on why it is necessary and how to apply it in practical applications.
In practice, section properties are often calculated on Excel spreadsheets for various reasons.
Concrete is divided into rectangular or triangular sections and calculated by assigning numbers to each section while steel is calculated by naming each plate. This is based on the parallel axis theorem.
Since it is a symmetrical section like below, there is not much of a problem with calculation as it is not difficult.
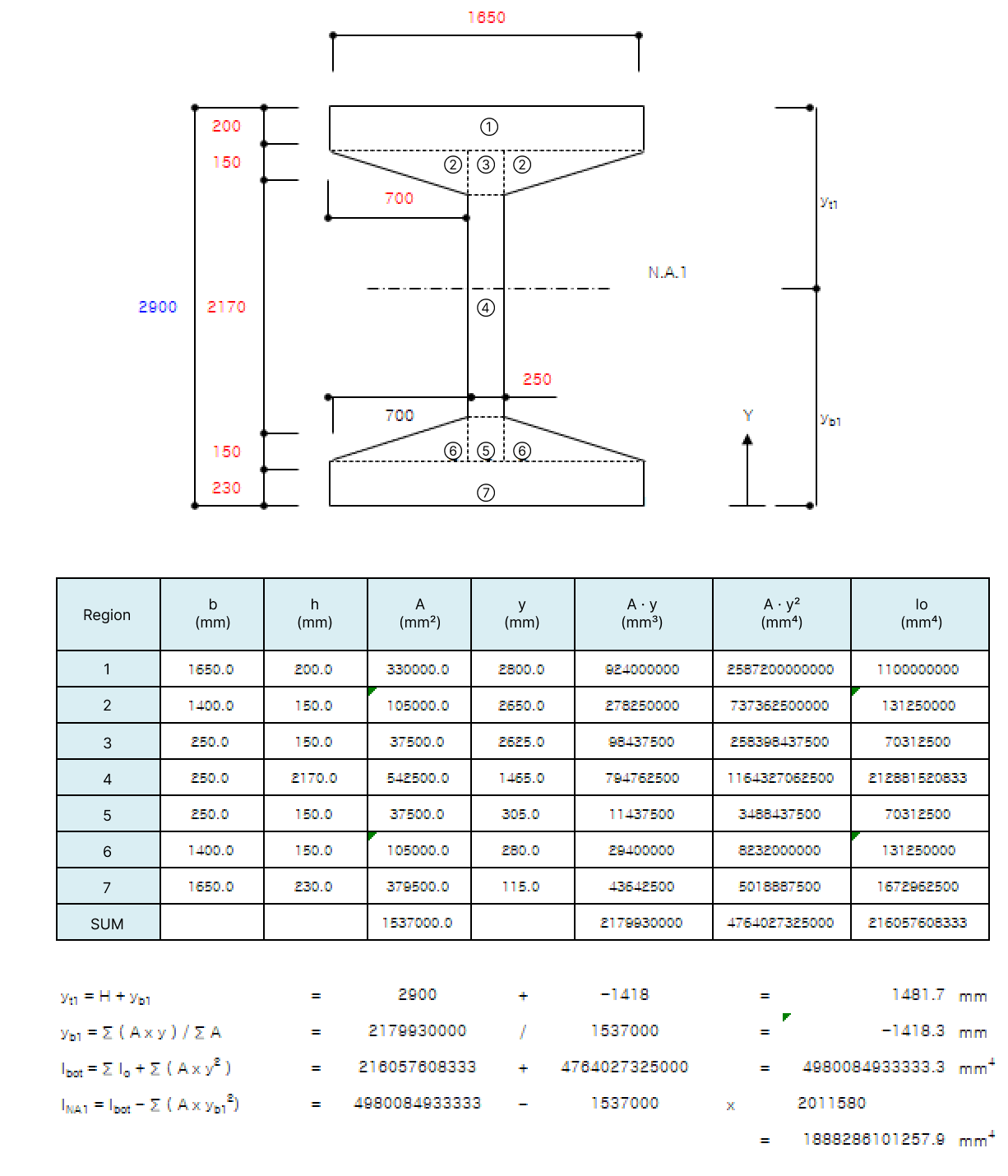
Figure 1-1. Section Calculation Examples
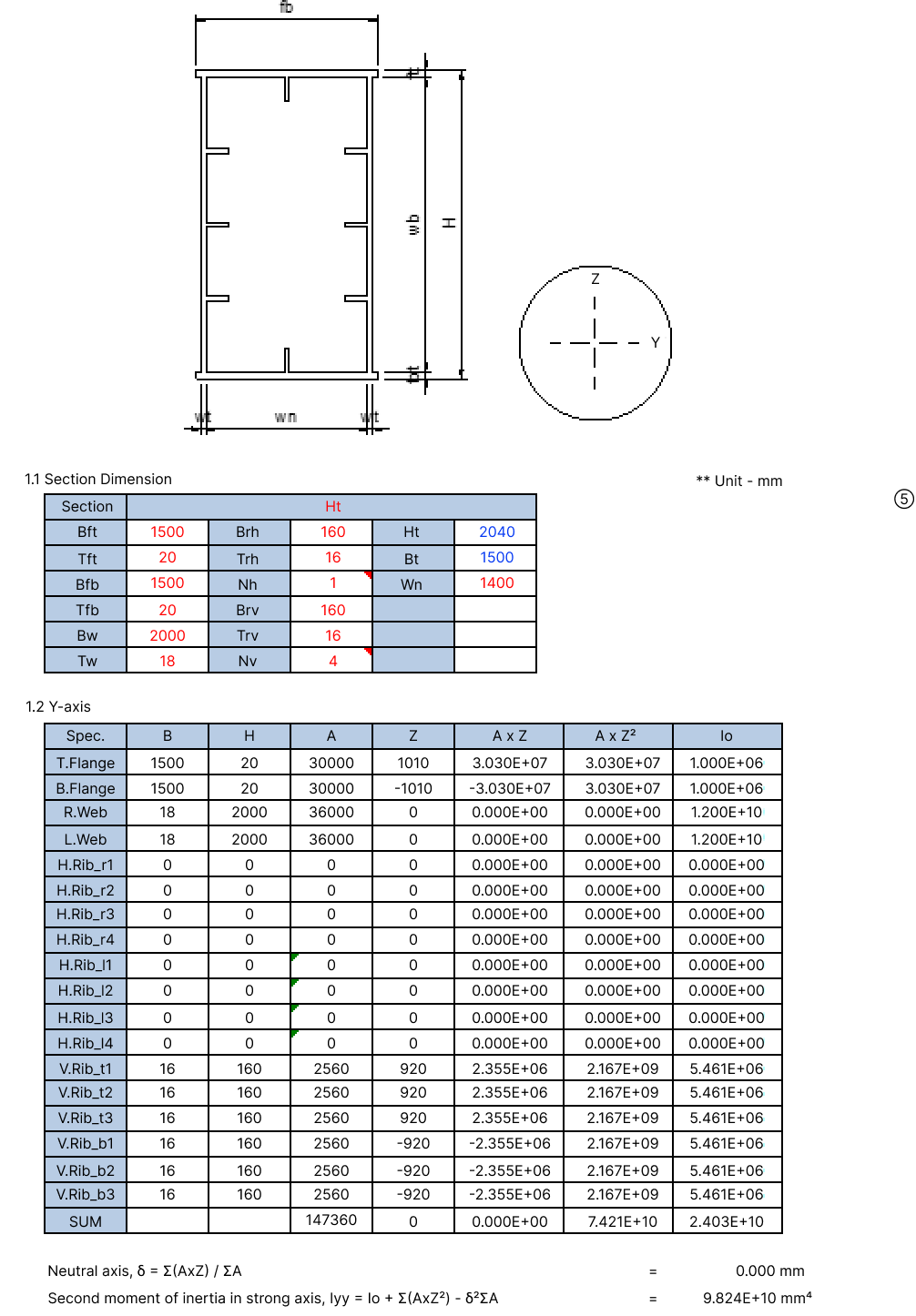
Figure 1-2. Section Calculation Examples
What if the contractor demands the use of wide-flange prestressed concrete (PSC) beams for the construction of a bridge, to showcase their construction capabilities? In any case, the cross-sectional shape is in the range of a typical PSC beam, and the flange width is only slightly asymmetric, which can be ignored at an acceptable level.
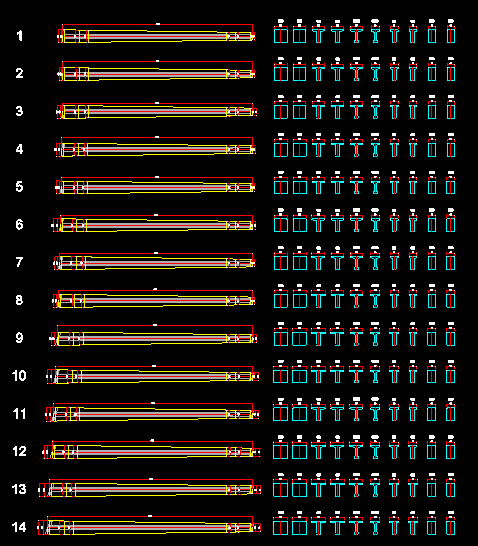Figure 2. Typical Sections of Prestressed Concrete Beams
What about cases like this? It can be solved with the "massprop" command in CAD or using a similar method. It is an open section and is asymmetric, which can lead to difficulties in design.
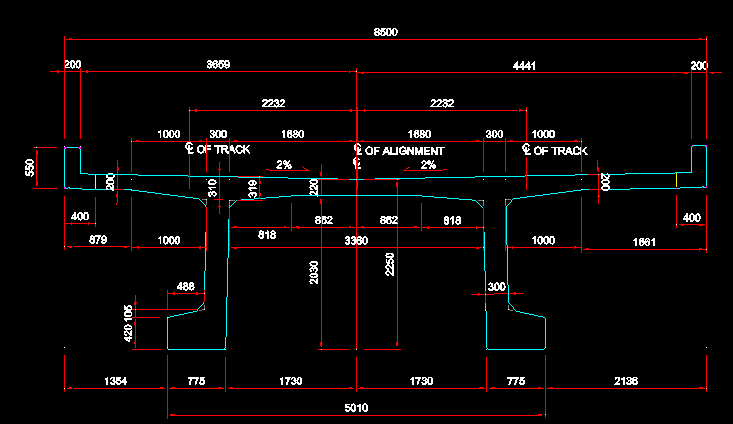
Figure 3. An Asymmetric Section Example
Doing the same work over and over made me feel like something new was needed.
So, after thinking and searching,
Figure 4. Thinking Process
There is a method called "Green's theorem" which can calculate section properties using continuous coordinates of a section.
(2) “Green’s Theorem”
Green's theorem in vector calculus establishes the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C. It is a special case of the more general Stokes' theorem, which applies to higher dimensions.
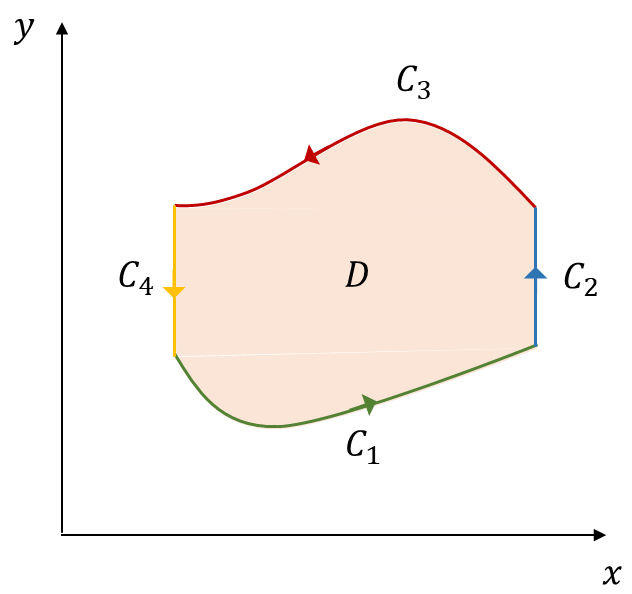
Figure 5. Green’s Theorem
If P and Q are continuously differentiable functions of (x,y) defined on an open region containing D, then the following equation holds and C is oriented counterclockwise:
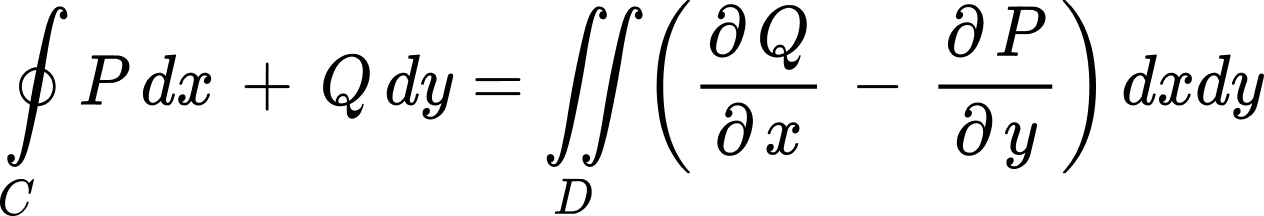
Calculation formula 1.
To calculate section properties, one cannot simply study vector calculus, as it is not an easy topic that can be studied easily. As we move on to the relevant content, we can confirm that we can calculate six properties (area, centroid, second moment of area, and section moduli) from continuous coordinates of a section.
